
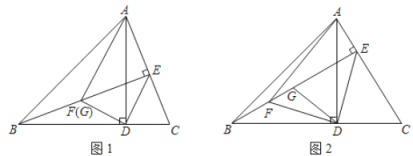
【题目】锐角△ABC 中,BC=6,BC 边上的高 AD=4,两动点 M,N 分别在边 AB,AC 上滑动(M 不与 A、B 重合),且 MN∥BC,以 MN 为边向下作正方形 MPQN,设其边长为 x,正方形 MPQN 与△ABC 公共部分的面积为 y(y>0).
(1)MN,BC具备什么条件,△AMN∽△ABC;
(2)当 x为何值时,PQ 恰好落在边 BC 上(如图 1);
(3)当 PQ 在△ABC 外部时(如图 2),求 y 关于 x 的函数关系式(注明 x 的取值范围)并求出 x 为何值时 y 最大,最大值是多少?

【答案】(1)MN∥BC;(2)x=![]() ;(3)当 x=3 时,y 有最大值,最大值是 6.
;(3)当 x=3 时,y 有最大值,最大值是 6.
【解析】
(1)根据 MN∥BC,得△AMN∽△ABC;(2)因为正方形的位置在变化,但是△AMN∽△ABC 没有改变,利用相似三角形对应边上高的比等于相似比,得出等量关系,代入解析式;(3)用含 x 的式子表示矩形 MEFN 边长,从而求出面积的表达式.
(1)∵MN∥BC,
∴△AMN∽△ABC;
(2)当 PQ 恰好落在边 BC上时,
∵MN∥BC,∴△AMN∽△ABC.
∴![]() ,
,
即 ![]() ,x=
,x= ![]() ;
;
(3)设 BC 分别交 MP,NQ 于 E,F,则四边形 MEFN 为矩形.
设 ME=NF=h,AD 交 MN 于 G(如图 2)GD=NF=h,AG=4﹣h.
∵MN∥BC,
∴△AMN∽△ABC.
∴![]() ,即
,即 ![]() ,
,
∴h=﹣![]() x+4.
x+4.
∴y=MNNF=x(﹣![]() x+4)=-
x+4)=-![]() x+4x(2.4<x<6),
x+4x(2.4<x<6),
配方得:y=﹣![]() (x﹣3)+6.
(x﹣3)+6.
∴当 x=3 时,y 有最大值,最大值是 6.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同。
(1)从箱子中任意摸出一个球是白球的概率是多少?
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 边上的高,连接
边上的高,连接![]() ,过点
,过点![]() 作
作![]() 与点
与点![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,
,![]() .
.
(1)如图![]() ,若点
,若点![]() 与点
与点![]() 重合,求证:
重合,求证:![]() ;
;
(2)如图![]() ,请写出
,请写出![]() 与
与![]() 之间的关系并证明.
之间的关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 是等边三角形,D 为 CB 延长线上一点,E 为 BC 延长线上点.
(1)当 BD、BC 和 CE 满足什么条件时,△ADB∽△EAC?
(2)当△ADB∽△EAC 时,求∠DAE 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中Rt△AOB≌Rt△DCA,其中B(0,4),C(2,0).连接BD.

(1)求直线BD的解析式;
(2)点E是直线AD上一点,连接BE,以BE,ED为一组邻边作BEDF,当BEDF的面积为3时,求点E的坐标;
(3)如图2,将△DAC沿x轴向左平移,平移距离大于0,记平移后的△DAC为△D′A′C′,连接D′A,D′B,当△D′AB为等腰三角形时,直接写出点D′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
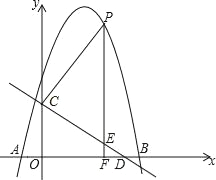
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,直线y=﹣![]() x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
(1)求抛物线的解析式;
(2)求PE的长最大时m的值.
(3)Q是平面直角坐标系内一点,在(2)的情况下,以PQCD为顶点的四边形是平行四边形是否存在?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com