
【题目】如图,△ABC 是等边三角形,D 为 CB 延长线上一点,E 为 BC 延长线上点.
(1)当 BD、BC 和 CE 满足什么条件时,△ADB∽△EAC?
(2)当△ADB∽△EAC 时,求∠DAE 的度数.

【答案】(1)见解析;(2)120°.
【解析】
(1)由等边三角形得 AB=BC=CA、∠ABC=∠ACB=60°,即∠ABD=∠ACE=120°,结合 BC=BDCE 知 ABAC=BDCE,据此可得答案;(2)由△ADB∽△EAC 知∠D=∠CAE,由∠ABC=∠D+∠DAB=60°知∠CAE+∠DAB=60°,根据∠DAE=∠CAE+∠DAB+∠BAC 可得答案.
(1)当 BC=BDCE 时,△ADB∽△EAC,
∵△ABC 是等边三角形,
∴AB=BC=CA,∠ABC=∠ACB=60°,
∴∠ABD=∠ACE=120°,
∵BC=BDCE,
∴ABAC=BDCE,
![]() ,
,
∴△ADB∽△EAC;
(2)∵△ADB∽△EAC,
∴∠D=∠CAE,
∵∠ABC=∠D+∠DAB=60°,
∴∠CAE+∠DAB=60°,
∴∠DAE=∠CAE+∠DAB+∠BAC=60°+60°=120°.


科目:初中数学 来源: 题型:
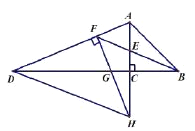
【题目】如图,在等腰直角![]() 中,
中,![]() ,
,![]() 的角平分线
的角平分线![]() 与
与![]() 的外角平分线
的外角平分线![]() 交于点
交于点![]() ,分别交
,分别交![]() 和
和![]() 的延长线于点
的延长线于点![]() ,
,![]() 过点
过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() 为等腰直角三角形:④
为等腰直角三角形:④![]() .其中正确的结论有__________.
.其中正确的结论有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.有两条边对应相等的两个三角形全等
B.两腰对应相等的两个等腰三角形全等
C.两角对应相等的两个等腰三角形全等
D.一边对应相等的两个等边三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
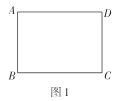
综合与实践课上,老师让同学们以“折纸”为主题开展数学活动.如图1,有一张长为4,宽为3的矩形纸片![]() (
(![]() ).
).
操作发现
(1)快乐小组先将图1中的矩形纸片![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 落在点
落在点![]() 处,得到图2,他们发现
处,得到图2,他们发现![]() ,请你证明这个结论;
,请你证明这个结论;
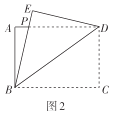
(2)创新小组将图2中的矩形纸片展开后继续折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ,得到图3,则折痕
,得到图3,则折痕![]() __________;
__________;
实践探究
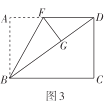
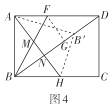
(3)前进小组在创新小组的操作基础上,将图3中的纸片展开,再将矩形纸片![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,然后将纸片展平.如图4所示,折痕
处,然后将纸片展平.如图4所示,折痕![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,试判断
,试判断![]() 的形状并证明你的结论.
的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两段材料,回答问题:
材料一:点A(x1,y1),B(x2,y2)的中点坐标为(![]() ,
,![]() ).例如,点(1,5),(3,﹣1)的中点坐标为(
).例如,点(1,5),(3,﹣1)的中点坐标为(![]() ,
,![]() ),即(2,2).
),即(2,2).
材料二:如图1,正比例函数l1:y=k1x和l2:y=k2x的图象相互垂直,分别在l1和l2上取点A,B,使得AO=BO.分别过点A,B作x轴的垂线,垂足分别为点C,D.显然,△AOC≌△OBD.设OC=BD=a,AC=OD=b,则A(﹣a,b),B(b,a).于是k1=﹣![]() ,k2=
,k2=![]() ,所以k1k2的值为一个常数.一般地,一次函数y=k1x+b1,y=k2x+b2可分别由正比例函数l1,l2平移得到.
,所以k1k2的值为一个常数.一般地,一次函数y=k1x+b1,y=k2x+b2可分别由正比例函数l1,l2平移得到.
所以,我们经过探索得到的结论是:任意两个一次函数y=k1x+b1,y=k2x+b2的图象相互垂直,则k1k2的值为一个常数.
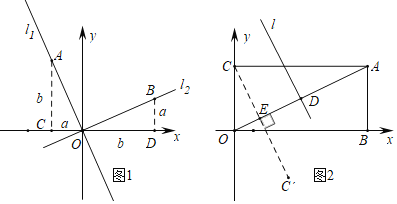
(1)在材料二中,k1k2= (写出这个常数具体的值);
(2)如图2,在矩形OBAC中A(4,2),点D是OA中点,用两段材料的结论,求点D的坐标和OA的垂直平分线l的解析式;
(3)若点C′与点C关于OA对称,用两段材料的结论,求点C′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】锐角△ABC 中,BC=6,BC 边上的高 AD=4,两动点 M,N 分别在边 AB,AC 上滑动(M 不与 A、B 重合),且 MN∥BC,以 MN 为边向下作正方形 MPQN,设其边长为 x,正方形 MPQN 与△ABC 公共部分的面积为 y(y>0).
(1)MN,BC具备什么条件,△AMN∽△ABC;
(2)当 x为何值时,PQ 恰好落在边 BC 上(如图 1);
(3)当 PQ 在△ABC 外部时(如图 2),求 y 关于 x 的函数关系式(注明 x 的取值范围)并求出 x 为何值时 y 最大,最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
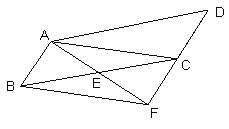
【题目】如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com