
 如图1,AB是⊙O的直径,点C、D在⊙O上两点,弧AC=弧CD,过点C作⊙O的切线,分别交BD、BA延长线于点E、P.
如图1,AB是⊙O的直径,点C、D在⊙O上两点,弧AC=弧CD,过点C作⊙O的切线,分别交BD、BA延长线于点E、P.| 5 |
| 2 |
| 3 |
| 2 |
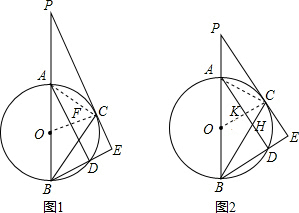 解:(1)连接OC,交AD于点F,连接AC,
解:(1)连接OC,交AD于点F,连接AC,| 1 |
| 2 |
| 1 |
| 2 |
| BC2-CE2 |
| BC |
| BE |
| BA |
| BC |
| BC2 |
| BE |
| 25 |
| 4 |
| AB2-AD2 |
| 7 |
| 4 |
 |
| AC |
 |
| CD |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| CK |
| AK |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 问题情境
问题情境| x |
|
|
|
|
1 | 2 | 3 | 4 | 5 | ||||||||
| y |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、了解全市中学生的心理健康状况 |
| B、了解某班同学“立定跳远”的成绩 |
| C、了解重庆市的空气质量情况 |
| D、了解端午节期间重庆市场上的粽子质量情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过点M作MN∥BC交AC于点N,以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过点M作MN∥BC交AC于点N,以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G.
如图,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com