
 如图,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G.
如图,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G.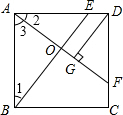 (1)证明:在正方形ABCD中,AB=AD=CD,∠BAD=∠ADC=90°,
(1)证明:在正方形ABCD中,AB=AD=CD,∠BAD=∠ADC=90°,
|
|


科目:初中数学 来源: 题型:
 如图1,AB是⊙O的直径,点C、D在⊙O上两点,弧AC=弧CD,过点C作⊙O的切线,分别交BD、BA延长线于点E、P.
如图1,AB是⊙O的直径,点C、D在⊙O上两点,弧AC=弧CD,过点C作⊙O的切线,分别交BD、BA延长线于点E、P.| 5 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 北京时间2013年4月20日8时02分四川省雅安市芦山县(北纬30.3,东经103.0)发生7.0级地震,空军某部队奉命赴灾区空投物资,已知空投物资离开飞机后在空中沿顶点为机舱舱口A的抛物线y=-
北京时间2013年4月20日8时02分四川省雅安市芦山县(北纬30.3,东经103.0)发生7.0级地震,空军某部队奉命赴灾区空投物资,已知空投物资离开飞机后在空中沿顶点为机舱舱口A的抛物线y=-| 1 |
| 250 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图正方形AOBC,等腰Rt△EOF中,∠EOF=90°,EF与OB交于G,连接AE、AB、BF.
如图正方形AOBC,等腰Rt△EOF中,∠EOF=90°,EF与OB交于G,连接AE、AB、BF.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

| A、只有①② | B、只有②③ |
| C、只有①③ | D、①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com