
| A. | 78 | B. | 30 | C. | 21 | D. | 12 |
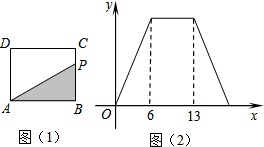
分析 根据三角形面积公式,可得当点P从B点运动到点C时,y随x的增大而增大;当点P从C点运动到点D时,y随x的增大而不变,此时y最大;当点P从D点运动到点A时,y随x的增大而减小,再结合函数图象可得BC=6,BC+CD=13,则CD=7,所以AB=7,然后根据三角形面积公式求y的最大值.
解答 解:当点P从B点运动到点C时,y随x的增大而增大;当点P从C点运动到点D时,y随x的增大而不变,此时y最大;当点P从D点运动到点A时,y随x的增大而减小;
由图(2)得点P从B点运动到点C时,路径为6,则BC=6;点P从B点运动到点D时路径为13,则CD=13-6=7,
所以AB=CD=7,
由于点P从C点运动到点D时,y最大,所以y的最大值=$\frac{1}{2}$×6×7=21.
故选C.
点评 本题考查了动点问题的函数图象:函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,要理清图象的含义即会识图.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第二、三、四象限 | D. | 第一、三、四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-1<b-1 | B. | -a<-b | C. | 2013a<2013b | D. | $\frac{a}{2014}$<$\frac{b}{2014}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AC=BC=2,∠ACB=90°,D是BC边的中点,E是AB边上一动点,则EC+ED的最小值是( )
如图,在△ABC中,AC=BC=2,∠ACB=90°,D是BC边的中点,E是AB边上一动点,则EC+ED的最小值是( )| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 3 | D. | 2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
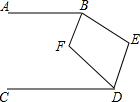 如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=140°.
如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=140°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com