
【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) | x60 | x |
售价(元/件) | 200 | 100 |
若用1800元购进甲种商品的件数与用900元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共100件,其中销售甲种商品为a件(a40),设销售完100件甲、乙两种商品的总利润为w元,求w与a之间的函数关系式,并求出w的最小值.
科目:初中数学 来源: 题型:
【题目】国务院发布的《全民科学素质行动计划纲要实施方案(2016-2020年)》指出:公民科学素质是实施创新驱动发展战略的基础,是国家综合国力的体现.《方案》明确提出,2020年要将我国公民科学素质的数值提升到10%以上.为了解我国公民科学素质水平及发展状况,中国科协等单位已多次组织了全国范围的调查,以下是根据调查结果整理得到的部分信息.注:科学素质的数值是指具备一定科学素质的公民人数占公民总数的百分比.
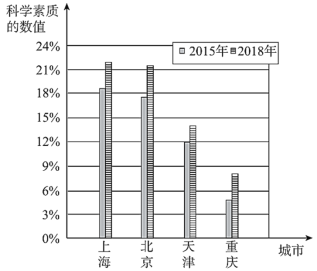
![]() .2015和2018年我国各直辖市公民科学素质发展状况统计图如下:
.2015和2018年我国各直辖市公民科学素质发展状况统计图如下:
b.2015年和2018年我国公民科学素质发展状况按性别分类统计如下:
2015年 | 2018年 | |
男 |
|
|
女 |
|
|
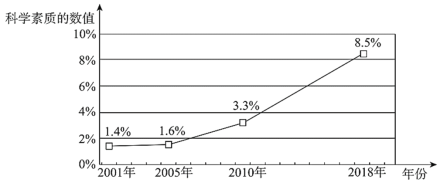
c.2001年以来我国公民科学素质水平发展统计图如下:
根据以上信息,回答下列问题:
(1)在我国四个直辖市中,从2015年到2018年,公民科学素质水平增幅最大的城市是________,公民科学素质水平增速最快的城市是_________.注:科学素质水平增幅=2018年科学素质的数值一2015年科学素质的数值;科学素质水平增速=(2018年科学素质的数值一2015年科学素质的数值)÷2015年科学素质的数值.
(2)已知在2015年的调查样本中,男女公民的比例约为1:1,则2015年我国公民的科学素质水平为______%(结果保留一位小数);由计算可知.在2018年的调查样本中.男性公民人数_____女性公民人数(填“多于”、“等于”或“少于”).
(3)根据截至2018年的调查数据推断,你认为“2020年我国公民科学素质提升到10%以上”的目标能够实现吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
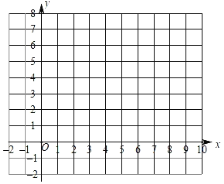
【题目】在平面直角坐标系xOy中,直线x=5与直线y=3,x轴分别交于点A,B,直线y=kx+b(k≠0)经过点A且与x轴交于点C(9,0).
(1)求直线y=kx+b的表达式;
(2)横、纵坐标都是整数的点叫做整点.记线段AB,BC,CA围成的区域(不含边界)为W.
①结合函数图象,直接写出区域W内的整点个数;
②将直线y=kx+b向下平移n个单位,当平移后的直线与区域W没有公共点时,请结合图象直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,AB,CD,EF,GH是正方形OPQR边上的线段,点M在其中某条线段上,若射线OM与x轴正半轴的夹角为α,且sinα>cosα,则点M所在的线段可以是( )
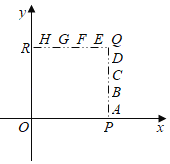
A.AB和CDB.AB和EFC.CD和GHD.EF和GH
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2+m的顶点为A.
(1)当m=1时,直接写出抛物线的对称轴;
(2)若点A在第一象限,且OA=![]() ,求抛物线的解析式;
,求抛物线的解析式;
(3)已知点B(m﹣![]() ,m+1),C(2,2).若抛物线与线段BC有公共点,结合函数图象,直接写出m的取值范围.
,m+1),C(2,2).若抛物线与线段BC有公共点,结合函数图象,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五张完全相同的卡片的正面分别画有等边三角形、平行四边形、矩形、菱形、正方形,将其背面朝上放在桌面上,从中随机抽取一张,所抽取的卡片上的图形既是轴对称图形,又是中心对称图形的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
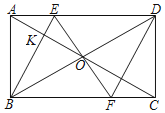
【题目】如图,在ABCD中,对角线AC,BD相交于点O,过点O作BD的垂线与边AD,BC分别交于点E,F,连接BE交AC于点K,连接DF.
(1)求证:四边形EBFD是菱形;
(2)若BK=3EK,AE=4,求四边形EBFD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
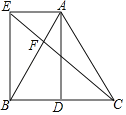
【题目】如图,在△ABC中,AB=AC,D为BC中点,AE∥BD,且AE=BD.
(1)求证:四边形AEBD是矩形;
(2)连接CE交AB于点F,若∠ABE=30°,AE=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=kx2+(2k+1)x+1(k为实数).
(1)对于任意实数k,函数图象一定经过点(﹣2,﹣1)和点_____;
(2)对于任意正实数k,当x>m时,y随着x的增大而增大,写出一个满足题意的m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com