
【题目】已知:关于x的一元二次方程mx2﹣(3m+2)x+2m+2=0(m>0)
(1)求证:方程有两个不相等的实数根且其中一根为定值.
(2)设方程的两个实数根分别为x1 , x2(其中x1<x2).若y是关于m的函数,且y=7x1﹣mx2 , 求这个函数的解析式;并求当自变量m的取值范围满足什么条件时,y≤3m.
【答案】
(1)证明:△=(3m+2)2﹣4m(2m+2)
=m2+4m+4
=(m+2)2,
∵m>0,
∴(m+2)2>0,即△>0,
∴方程有两个不相等的实数根,
∵x= ![]() ,
,
∴方程有一个根为1,
∴方程有两个不相等的实数根且其中一根为定值
(2)解:∵x= ![]() ,
,
∴x1=1,x2=2+ ![]() ,
,
∴y=7x1﹣mx2
=7﹣m(2+ ![]() )
)
=﹣2m+5,
当y≤3m,即﹣2m+5≤3m,
∴m≥1
【解析】(1)先计算判别式的值得到△=(m+2)2 , 由m>0,得到△>0,根据判别式的意义得到方程有两个不相等的实数根,再利用求根公式得到x= ![]() ,可得到方程有一个根为1,于是得到方程有两个不相等的实数根且其中一根为定值.(2)解方程得到x1=1,x2=2+
,可得到方程有一个根为1,于是得到方程有两个不相等的实数根且其中一根为定值.(2)解方程得到x1=1,x2=2+ ![]() ,所以y=7﹣m(2+
,所以y=7﹣m(2+ ![]() )=﹣2m+5,然后解不等式﹣2m+5≤3m.
)=﹣2m+5,然后解不等式﹣2m+5≤3m.
【考点精析】解答此题的关键在于理解求根公式的相关知识,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根,以及对根与系数的关系的理解,了解一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.


科目:初中数学 来源: 题型:
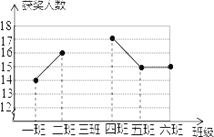
【题目】某中学组织网络安全知识竞赛活动,其中七年级6个班组每班参赛人数相同,学校对该年级的获奖人数进行统计,得到每班平均获奖15人,并制作成如图所示不完整的折线统计图.
(1)请将折线统计图补充完整,并直接写出该年级获奖人数最多的班级是 班;
(2)若二班获奖人数占班级参赛人数的32%,则全年级参赛人数是 人;
(3)若该年级并列第一名有男、女同学各2名,从中随机选取2名参加市级比赛,请用列表或画树状图的方法求出恰好选中一男一女的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P为Rt△ABC所在平面内任意一点(不在直线AC上),∠ACB=90°,M为AB边中点.操作:以PA、PC为邻边作平行四边形PADC,连续PM并延长到点E,使ME=PM,连接DE. 探究: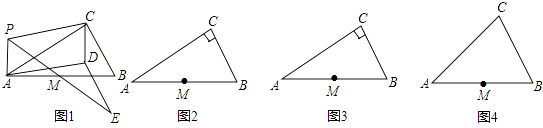
(1)请猜想与线段DE有关的三个结论;
(2)请你利用图2,图3选择不同位置的点P按上述方法操作;
(3)经历(2)之后,如果你认为你写的结论是正确的,请加以证明; 如果你认为你写的结论是错误的,请用图2或图3加以说明;
(注意:错误的结论,只要你用反例给予说明也得分)
(4)若将“Rt△ABC”改为“任意△ABC”,其他条件不变,利用图4操作,并写出与线段DE有关的结论(直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算甲、乙队的平均成绩和方差,试说明成绩较为整齐的是哪一队?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的图象如图所示,那么下面六个代数式:①abc;②b2-4ac;③a-b+c;④a+b+c;⑤2a-b;⑥9a-4b中,值小于0的有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知, 学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB,BC分别为线段,CD为双曲线的一部分).
(1)开始上课后第5分钟时与第30分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com