
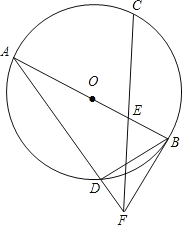
【题目】如图,AB是⊙O的直径,![]() ,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF.
,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF.
(1)求证:直线BF是⊙O的切线;
(2)若OB=2,求BD的长.
【答案】(1)证明见解析;(2)BD=![]() .
.
【解析】(1)连接OC,由已知可得∠BOC=90°,根据SAS证明△OCE≌△BFE,根据全等三角形的对应角相等可得∠OBF=∠COE=90°,继而可证明直线BF是⊙O的切线;
(2),由(1)的全等可知BF=OC=2,利用勾股定理求出AF的长,然后由S△ABF=![]() ,即可求出BD=
,即可求出BD=![]() .
.
(1)连接OC,
∵AB是⊙O的直径,![]() ,∴∠BOC=90°,
,∴∠BOC=90°,
∵E是OB的中点,∴OE=BE,
在△OCE和△BFE中,
 ,
,
∴△OCE≌△BFE(SAS),
∴∠OBF=∠COE=90°,
∴直线BF是⊙O的切线;
(2)∵OB=OC=2,由(1)得:△OCE≌△BFE,
∴BF=OC=2,
∴AF=![]() ,
,
∴S△ABF=![]() ,
,
即4×2=2![]() BD,
BD,
∴BD=![]() .
.


科目:初中数学 来源: 题型:
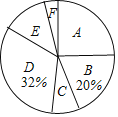
【题目】某校为了解学生最喜欢的球类运动情况,随机选取该校部分学生进行调查,要求每名学生只写一类最喜欢的球类运动.以下是根据调查结果绘制的统计图表的一部分.
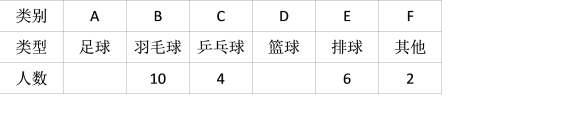
根据以上信息,解答下列问题:
(1)被调查的学生中,最喜欢乒乓球的有 人,最喜欢篮球的学生数占被调查总人数的百分比为 %;
(2)被调查学生的总数为 人,其中,最喜欢篮球的有 人,最喜欢足球的学生数占被调查总人数的百分比为 %;
(3)该校共有450名学生,根据调查结果,估计该校最喜欢排球的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
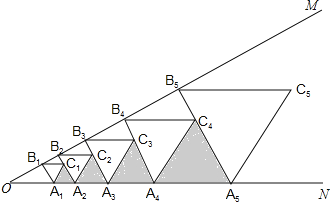
【题目】如图,∠MON=30°,点B1在边OM上,且OB1=2,过点B1作B1A1⊥OM交ON于点A1,以A1B1为边在A1B1右侧作等边三角形A1B1C1;过点C1作OM的垂线分别交OM、ON于点B2、A2,以A2B2为边在A2B2的右侧作等边三角形A2B2C2;过点C2作OM的垂线分别交OM、ON于点B3、A3,以A3B3为边在A3B3的右侧作等边三角形A3B3C3,…;按此规律进行下去,则△AnBn+1Cn的面积为__.(用含正整数n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句:①-1是1的平方根。②带根号的数都是无理数。③-1的立方根是-1。④![]() 的立方根是2。⑤(-2)2的算术平方根是2。⑥-125的立方根是±5。⑦有理数和数轴上的点一一对应。其中正确的有( )
的立方根是2。⑤(-2)2的算术平方根是2。⑥-125的立方根是±5。⑦有理数和数轴上的点一一对应。其中正确的有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入它所在的数集的括号里.
﹣![]() ,+5,﹣6.3,0,﹣
,+5,﹣6.3,0,﹣![]() ,2
,2![]() ,6.9,﹣7,210,0.031,﹣43,﹣10%
,6.9,﹣7,210,0.031,﹣43,﹣10%
正数集合:{ …}
整数集合:{ …}
非负数集合:{ …}
负分数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数a在数轴上表示的点在原点左侧,距离原点3个单位长,b在数轴上表示的点在原点右侧,距离原点2个单位长,c和d互为倒数,m与n互为相反数,y为最大的负整数,求(y+b)2+m(a-cd)-nb2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
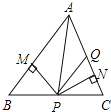
【题目】如图,在不等边![]() 中,
中,![]() ,垂足为M,
,垂足为M,![]() ,垂足为N,且
,垂足为N,且![]() ,点Q在AC上,
,点Q在AC上,![]() ,下列结论:
,下列结论:
![]() ,
,![]()
![]() ,
,![]()
![]() 平分
平分![]() ,
,![]()
![]() 平分
平分![]() ,
,
![]() ≌
≌![]() ,其中正确的个数有()
,其中正确的个数有()
A. 5个B. 4个C. 3个D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com