Question

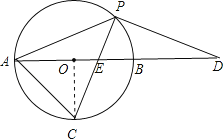
【题目】如图，以AB为直径的⊙O经过点P，C是⊙O上一点，连接PC交AB于点E，且∠ACP=60°，PA=PD．

（1）试判断PD与⊙O的位置关系，并说明理由；

（2）若：=1：2，求AE：EB：BD的值（请你直接写出结果）；

（3）若点C是弧AB的中点，已知AB=4，求CECP的值．

Answer 1

【答案】（1）PD与⊙O相切．理由见解析；（2）3：1：2（3）8

【解析】

试题分析：（1）连OP，根据圆周角定理得到∠AOP=2∠ACP=120°，则∠PAO=∠APO=30°，利用PA=PD得到∠D=∠PAD=30°，则∠APD=180°﹣30°﹣30°=120°，于是得到∠OPD=120°﹣30°=90°，根据切线的判定定理即可得到PD是⊙O的切线；

（2）连BC，由AB为直径，根据直径所对的圆周角为直角得到∠ACB=90°，利用：=1：2，则∠ABC=2∠BAC，所以有∠BAC=30°，∠ABC=60°，而∠PAE=30°，得到AE垂直平分PC，设BE=x，然后利用含30°的直角三角形三边的关系可求出AE：EB：BD的值；

（3）根据圆周角定理由弧AC=弧BC，得到∠CAB=∠APC，OC⊥AB，根据相似三角形的判定方法易得△ACE∽△PCA，则，即AC2=PCCE，利用勾股定理有A02+OC2=AC2=8，即可得到CECP的值．

解：（1）PD与⊙O相切．理由如下：

连接OP，

∵∠ACP=60°，

∴∠AOP=120°，

而OA=OP，

∴∠PAO=∠APO=30°，

∵PA=PD，

∴∠D=∠PAD=30°，

∴∠APD=180°﹣30°﹣30°=120°，

∴∠OPD=120°﹣30°=90°，

∵OP为半径，

∴PD是⊙O的切线；

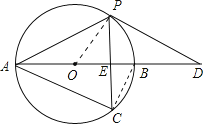
（2）连BC，

∵AB为直径，

∴∠ACB=90°，

∵：=1：2，

∴∠ABC=2∠BAC，

∴∠BAC=30°，∠ABC=60°，

而∠PAE=30°，

∴∠APE=∠DPE=60°，

∴AE垂直平分PC，如图，

设BE=x，在Rt△BCE中，∠BCE=30°，则BC=2BE=2x，

在Rt△ABC中，∠CAB=30°，AB=2BC=4x，

∴AE=AB﹣BE=3x，

∵PA=PD，PE⊥AD，

∴AE=DE，

∴DB=3x﹣x=2x，

∴AE：EB：BD的值为3：1：2；

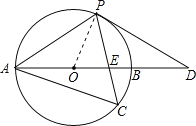
（3）如图，连接OC，

∵弧AC=弧BC，CO⊥AD，

∴∠CAB=∠APC，OC⊥AB，

而∠ACE=∠PCA，

∴△ACE∽△PCA，

∴，即AC2=PCCE，

∵A02+OC2=AC2=8，

∴PCCE=AC2=8．