
��ͼ1��A��B��C��DΪ���ε��ĸ����㣬AD=4cm��AB=dcm������E��F�ֱ�ӵ�D��B��������E��1cm/s���ٶ��ر�DA���A�ƶ�����F��1cm/s���ٶ��ر�BC���C�ƶ�����F�ƶ�����Cʱ������ͬʱֹͣ�ƶ�����EFΪ����������EFGH����F����xsʱ��������EFGH�����Ϊycm2����֪y��x�ĺ���ͼ���������ߵ�һ���֣���ͼ2��ʾ�������ͼ����Ϣ������������⣺
��1���Ա���x��ȡֵ��Χ����0��x��4����
��2��d=��3����m=��2����n=��25����
��3��F����������ʱ��������EFGH�����Ϊ16cm2��


�����㡿��������ĺ���ͼ��
��ר�⡿ѹ���⣻�����ͣ�
����������1�����ݾ��εĶԱ�������BC�ij���Ȼ������·�̡��ٶȡ�ʱ��Ĺ�ϵ��⼴�ɣ�
��2�����ݵ���˶���֪������E��F�ֱ��˶���AD��BC���е�ʱ�������ε������С�����d��m��ֵ���ٸ��ݿ�ʼ�ڽ���ʱ�����ε����������ù��ɶ������BD��ƽ������Ϊ���ֵn��
��3������E��EI��BC����Ϊ��I�����ı���DEICΪ���Σ�Ȼ���ʾ��EI��IF�������ù��ɶ�����ʾ��EF2�����������ε�����õ�y��x�ĺ�����ϵʽ��Ȼ���y=16�������x��ֵ�����ɵõ�ʱ�䣮
����𡿽⣺��1����BC=AD=4��4��1=4��
��0��x��4��
�ʴ�Ϊ��0��x��4��
��2���������⣬����E��F�ֱ��˶���AD��BC���е�ʱ��
EF=AB��������������EFGH���������
��ʱ��d2=9��m=4��2=2��
���ԣ�d=3��
���ݹ��ɶ�����n=BD2=AD2+AB2=42+32=25��
�ʴ�Ϊ��3��2��25��
��3����ͼ������E��EI��BC����Ϊ��I�����ı���DEICΪ���Σ�
��EI=DC=3��CI=DE=x��
��BF=x��
��IF=4��2x��
��Rt��EFI��EF2=EI2+IF2=32+��4��2x��2��
��y����EFΪ�߳���������EFGH�������
��y=32+��4��2x��2��
��y=16ʱ��32+��4��2x��2=16��
�����ã�4x2��16x+9=0��
��ã�x1=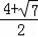
 ��x2=
��x2=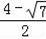
 ��
��
�ߵ�F���ٶ���1cm/s��
��F����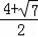
 ��
��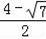
 ��ʱ��������EFGH�����Ϊ16cm2��
��ʱ��������EFGH�����Ϊ16cm2��
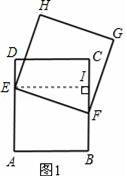

�����������⿼���˶�������ĺ���ͼ��2�����ݵ���ƶ�����϶��κ���ͼ���ҳ���EF=ABʱ�����ε����Ϊ��Сֵ�ǽ���Ĺؼ�����3�����������EFGH������ı���ʽ�ǽ���Ĺؼ���
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���Ե�OΪλ�����ģ�����ABC�Ŵ�õ���DEF����AD=OA�����ABC���DEF�����֮��Ϊ������


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
һ�κ���y=��3x+2��ͼ������������
A����һ���� B���ڶ����� C���������� D����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���в���ʽ������ȷ���ǣ�������
A����a��b��ac��bc B����a��b�é�2a����2b
C����a��b�é�a����b D����a��b��a��2��b��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
2001�����������������������з���������������Ͼ��У����������ǣ��˶�Ա��ͬʱ��ˮ��Ӿ1.5ǧ����һ����㣬�ڵ�һ�����������װ���������г���40ǧ���ڶ�����㣬���ܲ�10ǧ���յ㣮�±���2001����������������Ů���飨19�����£������˶�Ա�ڱ����еijɼ�����Ӿ�ɼ�����Ӿ����ʱ�䣬�������ƣ�����ʱ�䵥λΪ�룩
| �˶�Ա���� | ��Ӿ�ɼ� | ��һ���������ʱ�� | ���г��ɼ� | �ڶ����������ʱ�� | ���ܳɼ� |
| 191 | 1997 | 75 | 4927 | 40 | 3220 |
| 194 | 1503 | 110 | 5686 | 57 | 3652 |
| 195 | 1354 | 74 | 5351 | 44 | 3195 |
��1����գ���ȷ��0.01����
��191���˶�Ա�����г���ƽ���ٶ����� ����/�룻
��194���˶�Ա�����г���ƽ���ٶ����� ����/�룻
��195���˶�Ա�����г���ƽ���ٶ����� ����/�룻
��2������˶�Ա�����г��������ٵģ���ô�������г���;�У�191���˶�Ա����195�Ż�194��������ᣬ��ô��ʱ���һ������ж����ף���ȷ��0.01����������ᣬΪʲô��
��3���������Ҳ�������ٵģ���ô�ڳ���;���������˶�Ա���п���ij����ij����Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��AC�Ǿ���ABCD�ĶԽ��ߣ�AB=2��BC=2
 ����E��F�ֱ����߶�AB��AD�ϵĵ㣬����CE��CF������BCE=��ACF����CE=CFʱ��AE+AF=������
����E��F�ֱ����߶�AB��AD�ϵĵ㣬����CE��CF������BCE=��ACF����CE=CFʱ��AE+AF=������


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
2015�괺���ڼ䣬ȫ����23.2���˴ν��ж����ϱ����������ÿ�ѧ��������ʾ23.2���ǣ�������
A��23.2��108 B��2.32��109 C��232��107 D��2.32��108
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��AB�ǡ�O��ֱ����AC�ǡ�O�����ߣ�AΪ�е㣬����BC������ABC=45�㣬�����н�����ȷ���ǣ�������


A��AC��AB B��AC=AB C��AC��AB D��AC=
 BC
BC
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com