Question

11．如图，有一块边长为a的正三角形纸板，在它的三个角处分别截去一个彼此全等的筝行，再沿图中虚线折起，做成一个无盖的直三棱柱纸盒，若该纸盒侧面积的最大值是$\frac{9\sqrt{3}}{8}$cm²，则a的值为3cm．

Answer 1

分析 如图，由等边三角形的性质可以得出∠A=∠B=∠C=60°，由三个筝形全等就可以得出AD=BE=BF=CG=CH=AK，根据折叠后是一个三棱柱就可以得出DO=PE=PF=QG=QH=OK，四边形ODEP、四边形PFGQ、四边形QHKO为矩形，且全等．连结AO证明△AOD≌△AOK就可以得出∠OAD=∠OAK=30°，设OD=x，则AO=2x，由勾股定理就可以求出AD=$\sqrt{3}x$，由矩形的面积公式就可以表示纸盒的侧面积，由二次函数的性质得到其最大值的代数式，根据题意列方程，解方程即可．

解答 解：如图，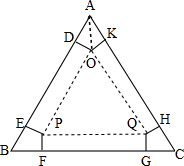

∵△ABC为等边三角形，
∴∠A=∠B=∠C=60°，AB=BC=AC．
∵筝形ADOK≌筝形BEPF≌筝形AGQH，
∴AD=BE=BF=CG=CH=AK．
∵折叠后是一个三棱柱，
∴DO=PE=PF=QG=QH=OK，四边形ODEP、四边形PFGQ、四边形QHKO都为矩形．
∴∠ADO=∠AKO=90°．
连结AO，
在Rt△AOD和Rt△AOK中，
$\left\{\begin{array}{l}{AO=AO}\\{OD=OK}\end{array}\right.$，
∴Rt△AOD≌Rt△AOK（HL）．
∴∠OAD=∠OAK=30°．
设OD=x，则AO=2x，由勾股定理就可以求出AD=$\sqrt{3}$x，
∴DE=a-$2\sqrt{3}$x，
∴纸盒侧面积=3x（a-2$\sqrt{3}$x）=-6$\sqrt{3}$x²+3ax=-6$\sqrt{3}$（x-$\frac{\sqrt{3}}{12}a$）²+$\frac{3\sqrt{3}{a}^{2}}{24}$，
∵该纸盒侧面积的最大值是$\frac{9\sqrt{3}}{8}$cm²，
∴$\frac{3\sqrt{3}{a}^{2}}{24}$=$\frac{9\sqrt{3}}{8}$，解得：a=3，或a=-3（舍去）；
故答案为：3．

点评 本题考查了等边三角形的性质的运用，全等三角形的判定及性质的运用，勾股定理的运用，矩形的面积公式的运用，二次函数的性质的运用，解答时表示出纸盒的侧面积是关键．