
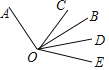
【题目】如图,已知OA⊥OB,点O为垂足,OC是∠AOB内任意一条射线,OB,OD分别平分∠COD,∠BOE,下列结论:①∠COD=∠BOE;②∠COE=3∠BOD;③∠BOE=∠AOC;④∠AOC与∠BOD互余,其中正确的有______(只填写正确结论的序号).
【答案】①②④
【解析】
由角平分线将角分成相等的两部分.结合选项得出正确结论.
解:①∵OB,OD分别平分∠COD,∠BOE,
∴∠COB=∠BOD=∠DOE,
设∠COB=x,
∴∠COD=2x,∠BOE=2x,
∴∠COD=∠BOE,
故①正确;
②∵∠COE=3x,∠BOD=x,
∴∠COE=3∠BOD,
故②正确;
③∵∠BOE=2x,∠AOC=90°-x,
∴∠BOE与∠AOC不一定相等,
故③不正确;
④∵OA⊥OB,
∴∠AOB=∠AOC+∠COB=90°,
∵∠BOC=∠BOD,
∴∠AOC与∠BOD互余,
故④正确,
∴本题正确的有:①②④;
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分;…;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,我们就称∠BAC是△ABC的好角.

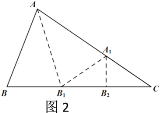
(1)如图2,在△ABC中,∠B>∠C,若经过两次折叠,∠BAC是△ABC的好角,则∠B与∠C的等量关系是_______;
(2)如果一个三角形的最小角是20°,则此三角形的最大角为______时,该三角形的三个角均是此三角形的好角。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业接到为地震灾区生产活动房的任务,此企业拥有九个生产车间,现在每个车间原有的成品活动房一样多,每个车间的生产能力也一样.有A、B两组检验员,其中A组有8名检验员前两天时间将第一、二车间的所有成品(原来的和这两天生产的)检验完毕后,再去检验第三、四车间所有成品,又用去三天时间;同时这五天时间B组检验员也检验完余下的五个车间的所有成品.如果每个检验员的检验速度一样快,那么B组检验员人数为( )
A. 8人B. 10人C. 12人D. 14人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学为了了解孩子们对《中国诗词大会》,《挑战不可能》,《最强大脑》,《超级演说家》,《地理中国》五种电视节目的喜爱程度,随机在七、八、九年级抽取了部分学生进行调查(每人只能选择一种喜爱的电视节目),并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题: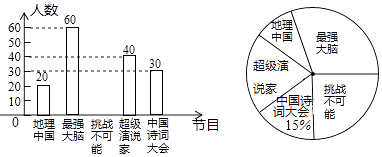
(1)本次调查中共抽取了名学生.
(2)补全条形统计图.
(3)在扇形统计图中,喜爱《地理中国》节目的人数所在的扇形的圆心角是度.
(4)若该学校有2000人,请你估计该学校喜欢《最强大脑》节目的学生人数是多少人?.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,过点D作DE⊥BD交BA的延长线于点E.
(1)当ABCD是菱形时,证明:AE=AB;
(2)当ABCD是矩形时,设∠E=α,问:∠E与∠DOA满足什么数量关系?写出结论并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y= ![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.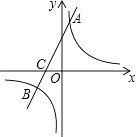
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图所示的竖式与横式两种无盖的长方形纸箱.(加工时接缝材料不计)

若该厂购进正方形纸板1000张,长方形纸板2000张.问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完;
该工厂某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试求在这一天加工两种纸盒时,a的所有可能值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com