
����Ŀ����ͼ1����ABC�У�����BAC��ƽ����AB1�۵��������ص����֣������²�������B1A1C��ƽ����A1B2�۵��������ص����֣����������²�������BnAnC��ƽ����AnBn+1�۵�����Bn���C�غϣ������۵����ٴΣ�ֻҪ���һ��ǡ���غϣ����Ǿͳ���BAC����ABC�ĺý�.

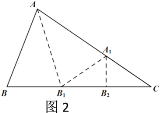
��1����ͼ2������ABC�У���B>��C�������������۵�����BAC����ABC�ĺýǣ�����B����C�ĵ�����ϵ��_______��
��2�����һ�������ε���С����20������������ε�����Ϊ______ʱ���������ε������Ǿ��Ǵ������εĺýǡ�
���𰸡�![]() 140����120����80��
140����120����80��
��������
��1�������۵����ʿɵá�A1B1B2=��C����AA1B1=��B����������������ʿɵá�AA1B1=2��C�����ݵ��������ɵá�B=2��C����2����������������۵�����BAC����ABC�ĺý�ʱ����B���C�ĵ�����ϵΪ��B=3��C�������ɵþ���n���۵�����BAC����ABC�ĺý�ʱ��B���C�ĵ�����ϵΪ��B=n��C����Ϊ��С����20������ABC�ĺýǣ����ݺýǶ��壬�������Ƿֱ�Ϊ20m��4mn�����������20m+20mn+20=180��������m(n+1)=8���ٸ���m��n�����������ɵ�m��n+1��8���������ӣ��Ӷ�������ý����
��1�������۵����ʵá�B=��AA1B1����A1B1B2=��C��
�ߡ�AA1B1=��A1B1B2+��C��
���B=2��C
�ʴ�Ϊ����B=2��C
��2����ͼ���߸����۵�������֪����B=��AA1B1����C=��A2B2C����A1B1C=��A1A2B2��
����������ε���Ƕ���֪����A1A2B2=��C+��A2B2C=2��C��
�߸����ı��ε���Ƕ���֪����BAC+��B+��AA1B1-��A1B1C=��BAC+2��B-2��C=180����
����������ABC���ڽǺͶ���֪����BAC+��B+��C=180����
���B=3��C��

�൱��B=2��Cʱ����BAC����ABC�ĺýǣ�����B=3��Cʱ����BAC����ABC�ĺýǣ�
��������n���۵���BAC����ABC�ĺýǣ����B���C���������B����C��֮��ĵ�����ϵΪ��B=n��C��
����С��Ϊ20����
������������Ϊ20m����20mn����
��20��+20m��+20mn��=180������m(1+n)=8��
��m��n������
��m=1��1+n=8����m=2��1+n=4����m=4��1+n=2.
��ã�m=1��n=7��m=2��n=3��m=4��n=1��
����������Ϊ20����140����40����120����80����80����
�������������Ϊ140����120����80��ʱ�������Ǿ��Ǵ������εĺý�.
�ʴ�Ϊ��140����120����80��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������5��д�Ų�ͬ���ֵĿ�Ƭ���밴Ҫ������������⣺
![]()
![]() ������ȡ��2�ſ�Ƭ��ʹ��2�ſ�Ƭ�����ֵij˻������˻������ֵ��______��
������ȡ��2�ſ�Ƭ��ʹ��2�ſ�Ƭ�����ֵij˻������˻������ֵ��______��
![]() ������ȡ��2�ſ�Ƭ��ʹ��2�ſ�Ƭ���������������С�����̵���Сֵ��______��
������ȡ��2�ſ�Ƭ��ʹ��2�ſ�Ƭ���������������С�����̵���Сֵ��______��
![]() ������ȡ��4�ſ�Ƭ����������ѧ�ļ��㷽����д��������ͬ������ʽ��ʹ�ĸ����ֵļ�����Ϊ24��
������ȡ��4�ſ�Ƭ����������ѧ�ļ��㷽����д��������ͬ������ʽ��ʹ�ĸ����ֵļ�����Ϊ24��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ĸ�ڣ���һ����лĸ�Ľ��գ����������������ڹ�ϣ�������ִ���ĸ����Դ���������ҹ���ĸ�ڶ���ÿ��5�µĵڶ��������գ�����Ϊ����ȫУ���иж�ĸ��������ij��ͨ���ʾ��������ʽ����2018��5��13�ա�ĸ�ڡ��ڼ䣬����ȫ��ѧ����ĸ�ױ���ж��ķ�ʽ���е���ͳ�ƣ����������ͼ��

(1)����༶���ж�����ѧ����
(2)����ͳ��ͼ�У�����ĸ���������������ε�Բ�ĽǵĶ����Ƕ��٣�
(3)��ȫ����ͳ��ͼ��
(4)����У��ѧ��1500�ˣ����Ƹ�У�ж�����ѧ��ͨ������ĸ��һ������ӵ����������ж���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ���������� ![]() ��һ�κ���y=bx��c��ͬһ����ϵ�ڵ�ͼ������ǣ� ��
��һ�κ���y=bx��c��ͬһ����ϵ�ڵ�ͼ������ǣ� ��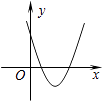
A.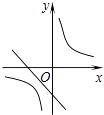
B.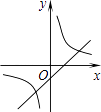
C.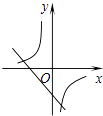
D.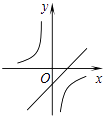
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=6����E�ڱ�CD�ϣ���CE=2DE������ADE��AE��������AFE���ӳ�EF����BC�ڵ�G������AG��CF�����н��ۣ�����ABG�ա�AFG����BG=GC����EG=DE+BG����AG��CF����S��FGC=3.6��������ȷ���۵ĸ����ǣ� ��

A��2 B��3 C��4 D��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
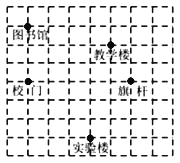
����Ŀ��ijѧУ��ƽ��ʾ��ͼ��ͼ��ʾ��ʵ��¥����λ�õ�����Ϊ(-2��-3)����ѧ¥����λ�õ�����Ϊ(-1��2)��
��1����ȷ��ͼ�������λ�õ����꣮
��2��ij����У��λ�ã����÷��������ķ�����ʾʵ��¥.
��3������ͼ�����У�ŵ��߶�����ƽ��5����λ����ƽ�ƺ���߶�������һ��������ʾ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
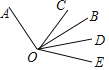
����Ŀ����ͼ����֪OA��OB����OΪ���㣬OC�ǡ�AOB������һ�����ߣ�OB��OD�ֱ�ƽ�֡�COD����BOE�����н��ۣ��١�COD=��BOE���ڡ�COE=3��BOD���ۡ�BOE=��AOC���ܡ�AOC���BOD���࣬������ȷ����______��ֻ��д��ȷ���۵���ţ���
�鿴�𰸺ͽ���>>
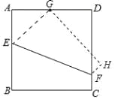
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ4��������ABCD�����ۺ�EF�۵���ʹ��B���ڱ�AD���е�G��.
(1)���߶�BE�ij���
(2)����BF��GF����֤��BF=GF��
(3)���ı���BCFE�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�BDƽ�֡�ABC��BC���д��߽�BC�ڵ�E����BD�ڵ�F������CF������A��60������ACF��42�������ABC��_____����
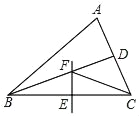
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com