
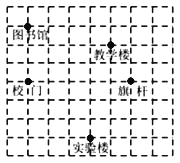
【题目】某学校的平面示意图如图所示,实验楼所在位置的坐标为(-2,-3),教学楼所在位置的坐标为(-1,2),
(1)请确定图书馆所在位置的坐标.
(2)某人在校门位置,请用方向与距离的方法表示实验楼.
(3)连接图书馆与校门的线段向右平移5个单位,则平移后的线段上任意一点怎样表示?
![]()
【答案】(1)(-5,3);(2)在校门的南偏东45°方向,距离校门3![]() 个单位长度;(3)(0,y)(
个单位长度;(3)(0,y)(![]() )
)
【解析】
(1)先根据实验楼所在位置的坐标和教学楼所在位置的坐标确定符合条件的平面直角坐标系,即可确定图书馆所在位置的坐标;(2)根据校门和实验楼的位置的坐标,得出方向角,根据勾股定理求出距离即可;(3)求出平移后的坐标,根据坐标位置表示出线段上的点的坐标即可.
(1)∵实验楼所在位置的坐标为(-2,-3),教学楼所在位置的坐标为(-1,2),
∴如图建立坐标系,
∴图书馆所在位置的坐标为(-5,3)
(2)如图,∵AB=3,BC=3,
∴∠BAC=45°,AC=![]() =3
=3![]()
∴在校门的南偏东45°方向,距离校门3![]() 个单位长度;
个单位长度;
(3)∵图书馆坐标为(-5,3),校门坐标为(-5,0),
∴向右平移5个单位后的坐标分别为(0,3)和(0,0)
∴平移后的线段上的任意点的坐标为(0,y)(0≤y≤3)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某市电力部门对一般照明用电实行“阶梯电价”收费,具体收费标准如下:
第一档:月用电量不超过200度的部分的电价为每度![]() 元.
元.
第二档:月用电量超过200度但不超过400度部分的电价为每度![]() 元.
元.
第三档:月用电量超过400度的部分的电价为每度![]() 元.
元.
![]() 已知小明家去年5月份的用电量为215度,则小明家5月份应交电费______元
已知小明家去年5月份的用电量为215度,则小明家5月份应交电费______元![]()
![]() 若去年6月份小明家用电的平均电价为
若去年6月份小明家用电的平均电价为![]() 元,求小明家去年6月份的用电量.
元,求小明家去年6月份的用电量.
![]() 已知小明家去年7、8月份的用电量共700度
已知小明家去年7、8月份的用电量共700度![]() 月份的用电量少于8月份的用电量
月份的用电量少于8月份的用电量![]() ,两个月的总电价是384元,求小明家7、8月的用电量分别是多少?
,两个月的总电价是384元,求小明家7、8月的用电量分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用棋子按照一定规律摆放图形
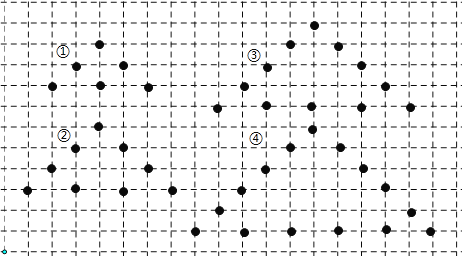
按照这种方式继续摆放下去,若摆放一个图形用去21枚棋子,则是摆放的第______个图形;摆放前n(n为正整数)个图形共需用______枚棋子.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节逛“大庙会“已成为成都老百姓的年俗,每年成都武侯祠博物馆举办的成都大庙会都会吸引大量的游客前往参观游玩.武侯祠大街某商家抓住商机采购了一批玩具熊猫,按成本价提高50%后标价,为了增加销量,又以9折优惠进行销售,每个售价为108元.
(1)这批玩具熊猫每个的成本价是多少元?
(2)这批玩具熊猫按此售价卖出三分之二以后,商家清仓换新,决定将剩下的玩具熊猫以每个72元的价格出售,若销售完这批玩具熊猫该商家共盈利4800元,求这批玩具熊猫的采购数量和销售利润率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分;…;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,我们就称∠BAC是△ABC的好角.

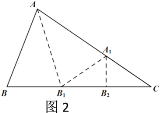
(1)如图2,在△ABC中,∠B>∠C,若经过两次折叠,∠BAC是△ABC的好角,则∠B与∠C的等量关系是_______;
(2)如果一个三角形的最小角是20°,则此三角形的最大角为______时,该三角形的三个角均是此三角形的好角。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四条直线l1:y1= ![]() x,l2:y2=
x,l2:y2= ![]() x,l3:y3=﹣
x,l3:y3=﹣ ![]() x,l4:y4=﹣
x,l4:y4=﹣ ![]() x,OA1=1,过点A1作A1A2⊥x轴,交l1于点A2 , 再过点A2作A2A3⊥l1交l2于点A3 , 再过点A3作A3A4⊥l2交y轴于点A4…,则点A2017坐标为 .
x,OA1=1,过点A1作A1A2⊥x轴,交l1于点A2 , 再过点A2作A2A3⊥l1交l2于点A3 , 再过点A3作A3A4⊥l2交y轴于点A4…,则点A2017坐标为 . 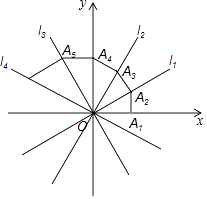
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学为了了解孩子们对《中国诗词大会》,《挑战不可能》,《最强大脑》,《超级演说家》,《地理中国》五种电视节目的喜爱程度,随机在七、八、九年级抽取了部分学生进行调查(每人只能选择一种喜爱的电视节目),并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题: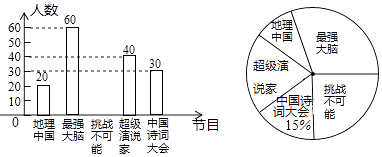
(1)本次调查中共抽取了名学生.
(2)补全条形统计图.
(3)在扇形统计图中,喜爱《地理中国》节目的人数所在的扇形的圆心角是度.
(4)若该学校有2000人,请你估计该学校喜欢《最强大脑》节目的学生人数是多少人?.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上,线段OA、OC的长度满足方程|x﹣15|+ ![]() =0(OA>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD=
=0(OA>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD= ![]()
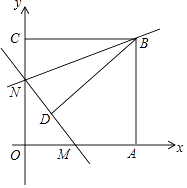
(1)求点B的坐标;
(2)求直线BN的解析式;
(3)将直线BN以每秒1个单位长度的速度沿y轴向下平移,求直线BN扫过矩形AOCB的面积S关于运动的时间t(0<t≤13)的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣ ![]() +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).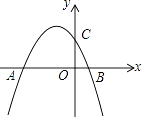
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com