
【题目】已知抛物线y=﹣ ![]() +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).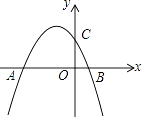
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
【答案】
(1)解:抛物线的解析式为y=﹣ ![]() (x+4)(x﹣1),即y=﹣
(x+4)(x﹣1),即y=﹣ ![]() x2﹣
x2﹣ ![]() x+2
x+2
(2)解:存在.
当x=0,y═﹣ ![]() x2﹣
x2﹣ ![]() x+2=2,则C(0,2),
x+2=2,则C(0,2),
∴OC=2,
∵A(﹣4,0),B(1,0),
∴OA=4,OB=1,AB=5,
当∠PCB=90°时,
∵AC2=42+22=20,BC2=22+12=5,AB2=52=25
∴AC2+BC2=AB2
∴△ACB是直角三角形,∠ACB=90°,
∴当点P与点A重合时,△PBC是以BC为直角边的直角三角形,此时P点坐标为(﹣4,0);
当∠PBC=90°时,PB∥AC,如图1,
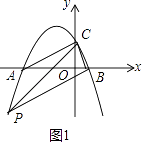
设直线AC的解析式为y=mx+n,
把A(﹣4,0),C(0,2)代入得 ![]() ,解得
,解得 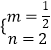 ,
,
∴直线AC的解析式为y= ![]() x+2,
x+2,
∵BP∥AC,
∴直线BP的解析式为y= ![]() x+p,
x+p,
把B(1,0)代入得 ![]() +p=0,解得p=﹣
+p=0,解得p=﹣ ![]() ,
,
∴直线BP的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
解方程组  得
得 ![]() 或
或 ![]() ,此时P点坐标为(﹣5,﹣3);
,此时P点坐标为(﹣5,﹣3);
综上所述,满足条件的P点坐标为(﹣4,0),P2(﹣5,﹣3)
(3)解:存在点E,设点E坐标为(m,0),F(n,﹣ ![]() n2﹣
n2﹣ ![]() n+2)
n+2)

①当AC为边,CF1∥AE1,易知CF1=3,此时E1坐标(﹣7,0),
②当AC为边时,AC∥EF,易知点F纵坐标为﹣2,
∴﹣ ![]() n2﹣
n2﹣ ![]() n+2=﹣2,解得n=
n+2=﹣2,解得n= ![]() ,得到F2(
,得到F2( ![]() ,﹣2),F3(
,﹣2),F3( ![]() ,﹣2),
,﹣2),
根据中点坐标公式得到: ![]() =
= ![]() 或
或 ![]() =
= ![]() ,
,
解得m= ![]() 或
或 ![]() ,
,
此时E2( ![]() ,0),E3(
,0),E3( ![]() ,0),
,0),
③当AC为对角线时,AE4=CF1=3,此时E4(﹣1,0),
综上所述满足条件的点E为(﹣7,0)或(﹣1,0)或( ![]() ,0)或(
,0)或( ![]() ,0)
,0)
【解析】(1)由抛物线经过A(﹣4,0),B(1,0).A、B在x轴上,所以可以设抛物线解析式为两根式:y=![]() (x+4)(x﹣1),展开整理即可;(2)注意分两种情况:①当∠PCB=90°时,②当∠PBC=90°时,不要遗漏情况;(3)分情况讨论:分AC为边,AC为对角线两种情况讨论.
(x+4)(x﹣1),展开整理即可;(2)注意分两种情况:①当∠PCB=90°时,②当∠PBC=90°时,不要遗漏情况;(3)分情况讨论:分AC为边,AC为对角线两种情况讨论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某学校的平面示意图如图所示,实验楼所在位置的坐标为(-2,-3),教学楼所在位置的坐标为(-1,2),
(1)请确定图书馆所在位置的坐标.
(2)某人在校门位置,请用方向与距离的方法表示实验楼.
(3)连接图书馆与校门的线段向右平移5个单位,则平移后的线段上任意一点怎样表示?
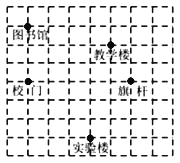
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交于A,B两点,点A和点B的横坐标分别为1和﹣2,这两点的纵坐标之和为1.
的图象与一次函数y=x+b的图象交于A,B两点,点A和点B的横坐标分别为1和﹣2,这两点的纵坐标之和为1.
(1)求反比例函数的表达式与一次函数的表达式;
(2)当点C的坐标为(0,﹣1)时,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ACF=42°,则∠ABC=_____°.
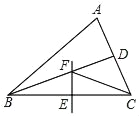
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把所有正奇数从小到大排列,并按如下规律分组:(1)(3,5,7)、(9,11,13,15,17),(19,21,23,25,27,29,31),…,现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A89=( )
A.(6,7)
B.(7,8)
C.(7,9)
D.(6,9)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图中二次函数解析式为y=ax2+bx+c(a≠0)则下列命题中正确的有(填序号)
①abc>0;②b2<4ac;③4a﹣2b+c>0;④2a+b>c.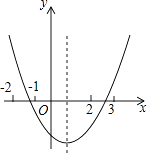
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张大小相同的长方形卡片(如图①)按图②、图③两种放法放在一个底面为长方形(长比宽多6)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为C2,图③中阴影部分的周长为C3,则C2-C3=______.
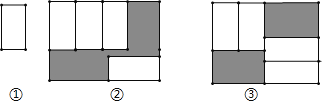
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com