
【题目】如图,正方形ABCD的对角线交于点O , 以AD为边向外作Rt△ADE , ∠AED=90°,连接OE , DE=6,OE= ![]() ,则另一直角边AE的长为( ).
,则另一直角边AE的长为( ).
A.![]()
B.2
C.8
D.10
【答案】D
【解析】过点O作OM⊥AE于点M , 作ON⊥DE , 交ED的延长线于点N , ∵∠AED=90°,∴四边形EMON是矩形,∵正方形ABCD的对角线交于点O , ∴∠AOD=90°,OA=OD , ∴∠AOD+∠AED=180°,∴点A , O , D , E共圆,∴∠AEO=∠DEO= ![]() ∠AED=45°,∴OM=ON , ∴四边形EMON是正方形,∴EM=EN=ON , ∴△OEN是等腰直角三角形,∵OE=
∠AED=45°,∴OM=ON , ∴四边形EMON是正方形,∴EM=EN=ON , ∴△OEN是等腰直角三角形,∵OE= ![]() ,∴EN=8,∴EM=EN=8,在Rt△AOM和Rt△DON中
,∴EN=8,∴EM=EN=8,在Rt△AOM和Rt△DON中 ![]() ,∴Rt△AOM≌Rt△DON(HL),∴AM=DN=EN-ED=8-6=2,∴AE=AM+EM=2+8=10.
,∴Rt△AOM≌Rt△DON(HL),∴AM=DN=EN-ED=8-6=2,∴AE=AM+EM=2+8=10.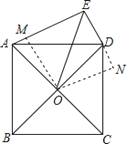
【考点精析】根据题目的已知条件,利用勾股定理的概念的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】下列各组线段中的三个长度:①9,12,15;②7,24,25;③32,42,52;④3a,4a,5a(a>0);⑤m2﹣n2,2mn,m2+n2(m,n为正整数,且m>n)其中可以构成直角三角形的有( )
A. 5组 B. 4组 C. 3组 D. 2组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.

(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品共用了160元.
(1)求A,B两种商品每件多少元?
(2)如果小亮准备购买A,B两种商品共10件,总费用不超过350元,且不低于300元,问有几种购买方案,哪种方案费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:
①b2>4ac ②2a+b=0 ③c﹣a<0 ④若点B(﹣4,y1)、C(1,y2)为函数图象上的两点,则y1<y2,其中正确结论是( )

A.②④ B.②③ C.①③ D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )
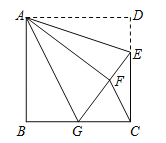
A.2 B.3 C.4 D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com