
【题目】如图,在菱形![]() 中,对角线
中,对角线![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向匀速运动,速度是
方向匀速运动,速度是![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向匀速运动,速度是
方向匀速运动,速度是![]() ,
,![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() .设运动时间为
.设运动时间为![]() .
.
(1)当![]() 于
于![]() 时,求
时,求![]() 的值;
的值;
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)是否存在某一时刻![]() ,使
,使![]() 平分
平分![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
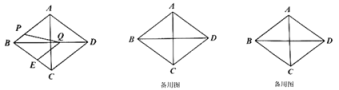
【答案】(1)当![]() 时
时![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时
时![]() 平分
平分![]() .
.
【解析】
(1)由题意得:![]() ,
,![]() ,
,![]() ,根据菱形的性质求出AO、BO、AB的值,再根据同角的余弦得出cos∠ABO
,根据菱形的性质求出AO、BO、AB的值,再根据同角的余弦得出cos∠ABO![]() ,代入计算即可求解;
,代入计算即可求解;
(2)过![]() 作
作![]() ,垂足为
,垂足为![]() ,根据同角的正弦弦得出sin∠ABO
,根据同角的正弦弦得出sin∠ABO![]() ,求出MQ,根据平行证出
,求出MQ,根据平行证出![]() ,由相似三角形的性质求出EQ,根据梯形的面积公式即可求得
,由相似三角形的性质求出EQ,根据梯形的面积公式即可求得![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)假设存在时刻![]() ,使
,使![]() 平分
平分![]() ,则
,则![]() ,过
,过![]() 作
作![]() ,垂足为
,垂足为![]() ,先证出△PBQ是等腰三角形,根据三线合一可得BN=
,先证出△PBQ是等腰三角形,根据三线合一可得BN=![]() BQ=4-t,再根据同角的余弦得出cos∠ABO
BQ=4-t,再根据同角的余弦得出cos∠ABO![]() ,代入计算即可求
,代入计算即可求![]() 的值.
的值.
解:(1)由题意得:![]() ,
,![]() ,
,![]() .
.
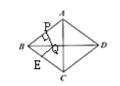
∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
假设存在![]() 使
使![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
得![]() .
.
∴当![]() 时
时![]() ;
;
(2)过![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
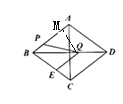
在![]() 中,
中,
![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,四边形BPQE是梯形,
,四边形BPQE是梯形,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)假设存在时刻![]() ,使
,使![]() 平分
平分![]() ,则
,则![]() ,
,
过![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
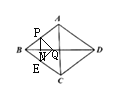
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
解得![]() .
.
∴当![]() 时
时![]() 平分
平分![]() .
.
故答案为:(1)当![]() 时
时![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时
时![]() 平分
平分![]() .
.


 核心素养学练评系列答案
核心素养学练评系列答案科目:初中数学 来源: 题型:
【题目】如图,P,Q是方格纸中的两格点,请按要求画出以PQ为对角线的格点四边形.
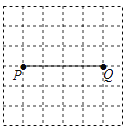
(1)在图1中画出一个面积最小的¨PAQB;
(2)在图2中画出一个四边形PCQD,使其是轴对称图形而不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.注:图1,图2在答题纸上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C与某建筑物底端B相距306米(点C与点B在同一水平面上),某同学从点C出发,沿同一剖面的斜坡CD行走195米至坡顶D处,斜坡CD的坡度(或坡比)i=1:2.4,在D处测得该建筑物顶端A的俯视角为20°,则建筑物AB的高度约为(精确到0.1米,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0364)____.
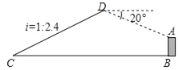
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的口袋中,装有3个分别标有数字1、2、3的小球,它们除标示的数字外完全相同,小红、小明和小亮用这些道具做摸球游戏.游戏规则如下:由小红随机从口袋中摸出一个小球,记录下数字,放回摇匀,再由小明随机从口袋中摸出一个小球,记录下数字,放回摇匀.如果两人摸到的小球上数字相同,那么小亮获胜;如果两人摸到的小球上数字不同,那么小球上数字大的一方获胜.
(1)请用树状图或列表的方法表示一次游戏中所有可能出现的结果;
(2)这个游戏规则对三人公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标;
(3)抛物线上是否存在一点Q(Q与B不重合),使△CDQ的面积等于△BCD的面积?若存在,直接写出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
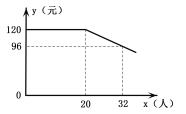
【题目】随着人们生活水平的提高,短途旅行日趋火爆.我市某旅行社推出“辽阳—葫芦岛海滨观光一日游”项目,团队人均报名费用y(元)与团队报名人数x(人)之间的函数关系如图所示,旅行社规定团队人均报名费用不能低于88元.旅行社收到的团队总报名费用为w(元).
(1)直接写出当x≥20时,y与x之间的函数关系式及自变量x的取值范围;
(2)儿童节当天旅行社收到某个团队的总报名费为3000元,报名旅游的人数是多少?
(3)当一个团队有多少人报名时,旅行社收到的总报名费最多?最多总报名费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.
(1)求购买该品牌一个台灯、一个手电筒各需要多少元?
(2)经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com