
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC,连结OB,D为OB的中点。点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF。已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒。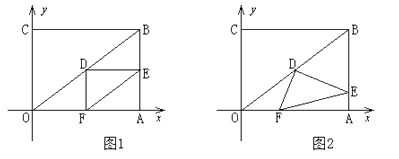
(1)如图1,当t=3时,求DF的长;
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值;
(3)连结AD,当AD将△DEF分成的两部分面积之比为1:2时,求相应t的值。
【答案】
(1)
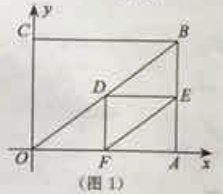
解:当t=3时,如图1,点E为AB中点.
∵点D为OB中点,
∴DE//OA,DE=![]() OA=4,
OA=4,
∵OA⊥AB,
∴DE⊥AB,
∴∠OAB=∠DEA=90°,
又∵DF⊥DE,
∴∠EDF=90°
∴四边形DFAE是矩形,
∴DF=AE=3.
(2)
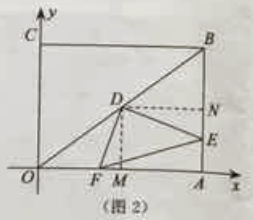
解: ∵∠DEF大小不变,如图2,
过D作DM⊥OA,DN⊥AB,垂足分别是M、N,
∵四边形OABC是矩形,
∴OA⊥AB,
∴四边形DMAN是矩形,
∴∠MDN=90°,DM//AB,DN//OA,
∴![]() ,
,![]() ,
,
∵点D为OB中点,
∴M、N分别是OA、AB中点,
∴DM=![]() AB=3,DN=
AB=3,DN=![]() OA=4,
OA=4,
∵∠EDF=90°,
∴∠FDM=∠EDN.
又∵∠DMF=∠DNE=90°,
∴△DMF∽△DNE
∴![]() ,
,
∵∠EDF=90°,
∴tan∠DEF=![]()
(3)
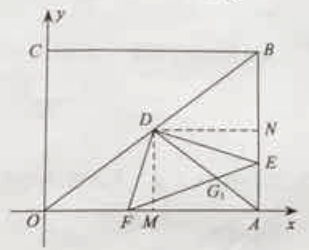
解:过D作DM⊥OA,DN⊥AB。垂足分别是M,N.
若AD将△DEF的面积分成1:2的两个部分,设AD交EF于点G,则易得点G为EF的三等分点.
①当点E到达中点之前时.
NE=3-t,由△DMF∽△DNE得
MF=![]() (3-t).
(3-t).
∴AF=4+MF=-![]() t+
t+![]() .
.
∵点![]() 为EF的三等分点。
为EF的三等分点。
∴![]() (
(![]() .
.![]() t).
t).
由点A(8,0),D(4,3)得直线AD解析式为y=-![]() χ+6.
χ+6.
![]() (
(![]() .
.![]() t)代入,得t=
t)代入,得t=![]() .
.
②当点E越过中点之后.
NE=t-3,由△DMF~△DNE得MF=![]() (t-3).
(t-3).
∴AF=4-MF=-![]() +
+![]() .
.
∵点![]() 为EF的三等分点.
为EF的三等分点.
∴![]() (
(![]() .
.![]() ).
).
代入直线AD解析式y=-![]() χ+6.
χ+6.
得t=![]() .
.
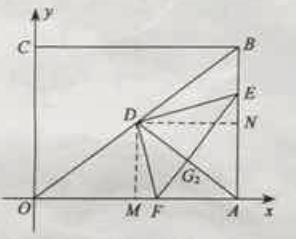
【解析】(1)当t=3时,如图1,点E、D分别为AB、OB中点,得出DE//OA,DE=![]() OA=4,根据OA⊥AB得出DE⊥AB,从而得出四边形DFAE是矩形,根据矩形性质求出DF=AE=3.
OA=4,根据OA⊥AB得出DE⊥AB,从而得出四边形DFAE是矩形,根据矩形性质求出DF=AE=3.
(2)如图2,过D作DM⊥OA,DN⊥AB,垂足分别是M、N,四边形OABC、DMAN都是矩形,由平行得出![]() ,
,![]() ,由D、M、N是中点又可以得出条件判断△DMF∽△DNE,从而得出tan∠DEF=
,由D、M、N是中点又可以得出条件判断△DMF∽△DNE,从而得出tan∠DEF=![]() 。
。
(3)过D作DM⊥OA,DN⊥AB。垂足分别是M,N;若AD将△DEF的面积分成1:2的两个部分,设AD交EF于点G,则易得点G为EF的三等分点.
分点E到达中点之前或越过中点之后来讨论,得出 NE,由△DMF∽△DNE得 MF和AF的长度, 再算出直线AD的解析式,由点G为EF的三等分点得出G点坐标将其代入AD直线方程求出t值。
【考点精析】本题主要考查了相似三角形的判定与性质和锐角三角函数的定义的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数才能正确解答此题.


科目:初中数学 来源: 题型:
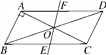
【题目】如图,在![]() ABCD中,AB⊥AC,AB=1,BC=
ABCD中,AB⊥AC,AB=1,BC=![]() ,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于E,F.
,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于E,F.
(1)求BD的长;
(2)当旋转角∠AOF=________° 时,△AOF与△BOE的面积相等?请写出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公司有三个住宅区可看作一点,A,B,C各区分别住有职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
![]()
A. 点A B. 点B
C. A,B之间 D. B,C之间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9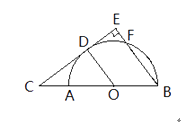
(1)求证:△COD∽△CBE;
(2)求半圆O的半径 ![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
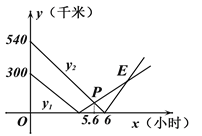
【题目】高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲乙两车离B的距离![]() 、
、![]() (千米)与行驶时间x(小时)之间的函数关系图象如图所示,交点P的横坐标为5.6,观察图象,给出下列结论:
(千米)与行驶时间x(小时)之间的函数关系图象如图所示,交点P的横坐标为5.6,观察图象,给出下列结论:
①A、C之间的路程为840千米;②乙车比甲车每小时快30千米;③当乙车到A点时,甲车距离B点250千米;④点E的坐标为(8,180).其中正确的有________________(填正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;

(2)若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丽水苛公司将“丽水山耕”农副产品运往杭州市场进行销售.记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市?请说明理由:
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
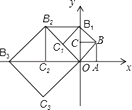
【题目】如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OBl为边作第三个正方形OBlB2C2,照此规律作下去,则点B2018的坐标为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com