
【题目】如图,△ABE为等腰直角三角形,∠ABE=90°,BC=BD,∠FAD=30°. 
(1)求证:△ABC≌△EBD;
(2)求∠AFE的度数.
【答案】
(1)证明:∵△ABE为等腰直角三角形,
∴AB=BE,
∵∠ABE=90°,
∴∠ABE=∠DBE=90°,
在△ABC与△BDE中,  ,
,
∴△ABC≌△EBD
(2)解:∵△ABC≌△EBD,
∴∠BAC=∠BED,
∵∠BED+∠D=90°,
∴∠BAC+∠D=90°,
∴∠AFD=90°,
∴∠AFE=90°
【解析】(1)根据等腰直角三角形的性质得到AB=BE,根据邻补角的定义得到∠ABE=∠DBE=90°,根据全等三角形的判定定理即可得到结论;(2)根据全等三角形的性质得到∠BAC=∠BED,根据三角形的内角和得到∠BED+∠D=90°,等量代换得到∠BAC+∠D=90°,即可得到结论.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点在格点上. 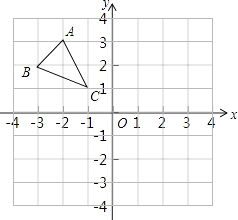
(1)作出与△ABC关于x轴对称的图形△A1B1C1;
(2)求出A1 , B1 , C1三点坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD=CB,E,F是AC上两动点,且有DE=BF. 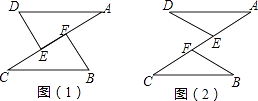
(1)若点E,F运动至如图(1)所示的位置,且有AF=CE,求证:△ADE≌△CBF;
(2)若点E,F运动至如图(2)所示的位置,仍有AF=CE,则△ADE≌△CBF还成立吗?为什么?
(3)若点E,F不重合,则AD和CB平行吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某灯具厂计划一天生产300盏景观灯,但由于各种原因,实际每天生产景观灯数与计划每天生产景观灯数相比有出入.下表是某周的生产情况(增产记为正、减产记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)求该厂本周实际生产景观灯的盏数;
(2)求产量最多的一天比产量最少的一天多生产景观灯的盏数;
(3)该厂实行每日计件工资制,每生产一盏景观灯可得60元,若超额完成任务,则超过部分每盏另奖20元,若未能完成任务,则少生产一盏扣25元,那么该厂工人这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中, 一块含60°角的三角板作如图摆放,斜边AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).
(1)请直接写出点B、C的坐标:B( , )、C( , );并求经过A、B、C三点的抛物线解析式;
(2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C. 此时,EF所在直线与(1)中的抛物线交于第一象限的点M.连接MB和MC,当△OCE∽△OBC时,判断四边形AEMC的形状,并给出证明;
(3)有一动点P在(1)中的抛物线上运动,是否存在点P,以点P为圆心作圆能和直线AC和x轴同时相切 ,若存在,求出圆心P的坐标;若不存在,请说明理由.
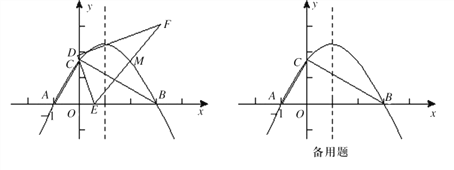
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市规定:出租车起步价允许行驶的最远路程为3千米,超过3千米的部分按每千米另行收费,甲说:“我乘这种出租车走了11千米,付了17元”;乙说:“我乘这种出租车走了23千米,付了35元”.请你算一算这种出租车的起步价是多少元?以及超过3千米后,每千米的车费是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com