
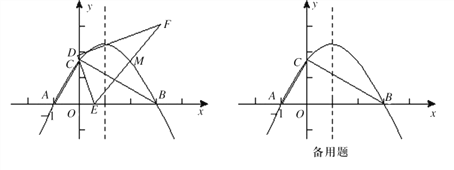
����Ŀ����ƽ��ֱ������ϵxoy�У� һ�麬60��ǵ����ǰ�����ͼ�ڷţ�б��AB��x���ϣ�ֱ�Ƕ���C��y���������ϣ���֪��A����1��0����
��1����ֱ��д����B��C�����꣺B�� �� ����C�� �� ��������A��B��C����������߽���ʽ��
��2���������������ǰ���ȫһ�������ǰ�DEF�����С�EDF=90�㣬��DEF=60�㣩���Ѷ���E�����߶�AB�ϣ���E�Dz���A��B�����غϵĶ��㣩����ʹED����ֱ�߾�����C�� ��ʱ��EF����ֱ���루1���е������߽��ڵ�һ���ĵ�M������MB��MC������OCE�ס�OBCʱ,�ж��ı���AEMC����״��������֤����
��3����һ����P�ڣ�1���е����������˶����Ƿ���ڵ�P���Ե�PΪԲ����Բ�ܺ�ֱ��AC��x��ͬʱ���� �������ڣ����Բ��P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��B��3��0����C��0�� ![]() ����A��B��C����������߽���ʽΪ
����A��B��C����������߽���ʽΪ![]() ��
��
��2���ı���AEMC�����Σ�֤����������
��3�����ڵ�P������������P����Ϊ��2�� ![]() ����6��-7
����6��-7![]() ��
��
����������1���⣺��1��B��3��0����C��0�� ![]() ����
����
��A����1��0��B��3��0����������A��B��C�����������Ϊ![]() ��
��
�֡�C��0�� ![]() �����������ϣ��࣬��ã�
�����������ϣ��࣬��ã�
�ྭ��A��B��C����������߽���ʽΪ![]() ��
��
��2���ı���AEMC�����Σ�
����OCE�ס�OBCʱ�������δ�ҵ�����Դ����
��OC=����δ�ҵ�����Դ������![]()
����δ�ҵ�����Դ����OE=1��
��E��1��0���������߶Գ����ϣ����CAEΪ�ȱ������Σ����AEC=��A=60�㣮
�֡ߡ�CEM=60�㣬 ���MEB=��AEC=60�㣮
���C���M���������ߵĶԳ���Գƣ�
C��0������δ�ҵ�����Դ��������M��2������δ�ҵ�����Դ������
��MC=AE=2�� MC��AE
���ı���AEMC��ƽ���ı��Ρ�
��AC=CM=2
���ı���AEMC�����Σ�
��3���ɡ�P��ֱ��AC��x��ͬʱ������֪��P�����нǵ�ƽ�����ϣ�
�ٵ���x���Ϸ�ʱ����PAO=30�㣬���P����Ϊ��x, ![]() ��,��P��PQ��x�ᣬ����ΪQ����AQ=
��,��P��PQ��x�ᣬ����ΪQ����AQ=![]() PQ,��x+1=
PQ,��x+1= ![]() (
(![]() )
)
��ã�x1=2 ,x2=-1(��ȥ)�����Ե�P����Ϊ��2�� ![]() ��
��
�ڵ���x���·�ʱ����PAO=60�㣬���P����Ϊ��x, ![]() ��,��P��PQ��x�ᣬ����ΪQ����
��,��P��PQ��x�ᣬ����ΪQ����![]() AQ=PQ,��
AQ=PQ,��![]() ��x+1��= -(
��x+1��= -(![]() )
)
��ã�x1=6 ,x2=-1(��ȥ)�����Ե�P����Ϊ��6��-7![]() ��
��
�������������ڵ�P������������P����Ϊ��2�� ![]() ����6��-7
����6��-7![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����䷽���ⷽ��x2��2x��1=0ʱ��ԭ����Ӧ����Ϊ�� ��
A.��x+1��2=2
B.��x+2��2=5
C.��x��1��2=2
D.��x��2��2=5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��������������1������1 �������n��������Щ�����ɫ�ⶼ��ͬ��
��1���Ӵ����������1����¼����ɫ��Żش����в����ȣ������ظ������飮�������������Ƶ���ȶ���0.75����n��ֵΪ ��
��2����n��2ʱ���Ѵ��е�����Ⱥ���������2������������2������ɫ��ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��B�������ϵ������㣬��A��ʾ����Ϊ13����B��ʾ����Ϊ��5������P�ӵ�B��������ÿ��4����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊ![]() �룮
�룮
��1��BP= ����P��ʾ���� ���ֱ��ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2����P�˶�������ʱ��PB=2PA��
��3����MΪBP���е㣬NΪPA���е㣬��P���˶��Ĺ����У��߶�MN�ij����Ƿ����仯�����仯����˵�����ɣ������䣬������߶�MN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABEΪ����ֱ�������Σ���ABE=90�㣬BC=BD����FAD=30�㣮 
��1����֤����ABC�ա�EBD��
��2�����AFE�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com