
【题目】在一个不透明袋子中有1个红球、1 个绿球和n个白球,这些球除颜色外都相同.
(1)从袋中随机摸出1个球,记录下颜色后放回袋子中并搅匀,不断重复该试验.发现摸到白球的频率稳定在0.75,则n的值为 ;
(2)当n=2时,把袋中的球搅匀后任意摸出2个球,求摸出的2个球颜色不同的概率.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答
(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E,F分别是边BC,CD上的点,且∠EAF= ![]() ∠BAD.
∠BAD.
求证:EF=BE+FD;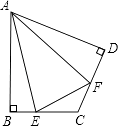
(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF= ![]() ∠BAD,(1)中的结论是否仍然成立?
∠BAD,(1)中的结论是否仍然成立? 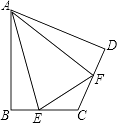
(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF= ![]() ∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明. 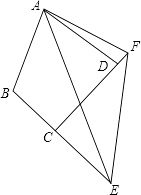
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD=CB,E,F是AC上两动点,且有DE=BF. 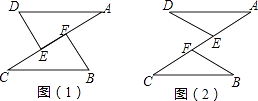
(1)若点E,F运动至如图(1)所示的位置,且有AF=CE,求证:△ADE≌△CBF;
(2)若点E,F运动至如图(2)所示的位置,仍有AF=CE,则△ADE≌△CBF还成立吗?为什么?
(3)若点E,F不重合,则AD和CB平行吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
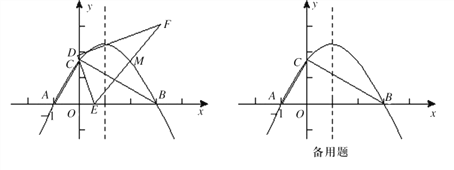
【题目】在平面直角坐标系xoy中, 一块含60°角的三角板作如图摆放,斜边AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).
(1)请直接写出点B、C的坐标:B( , )、C( , );并求经过A、B、C三点的抛物线解析式;
(2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C. 此时,EF所在直线与(1)中的抛物线交于第一象限的点M.连接MB和MC,当△OCE∽△OBC时,判断四边形AEMC的形状,并给出证明;
(3)有一动点P在(1)中的抛物线上运动,是否存在点P,以点P为圆心作圆能和直线AC和x轴同时相切 ,若存在,求出圆心P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com