
【题目】如图,AD=CB,E,F是AC上两动点,且有DE=BF. 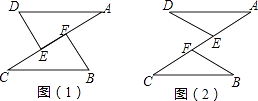
(1)若点E,F运动至如图(1)所示的位置,且有AF=CE,求证:△ADE≌△CBF;
(2)若点E,F运动至如图(2)所示的位置,仍有AF=CE,则△ADE≌△CBF还成立吗?为什么?
(3)若点E,F不重合,则AD和CB平行吗?请说明理由.
【答案】
(1)证明:∵AF=CE,
∴AF+EF=CE+EF,即AE=CF,
在△ADE和△CBF中,
∵ 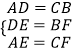 ,
,
∴△ADE≌△CBF(SSS)
(2)解:△ADE≌△CBF成立,
∵AF=CE,
∴AF﹣EF=CE﹣EF,即AE=CF,
在△ADE和△CBF中,
∵ 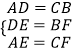 ,
,
∴△ADE≌△CBF(SSS)
(3)解:AD∥CB,
∵△ADE≌△CBF,
∴∠A=∠C,
∴AD∥CB
【解析】(1)由AF=CE知AF+EF=CE+EF,即AE=CF,又AD=CB、DE=BF可证△ADE≌△CBF;(2)由AF=CE知AF﹣EF=CE﹣EF,即AE=CF,又AD=CB、DE=BF可证△ADE≌△CBF;(3)根据(1)(2)可知△ADE≌△CBF,故∠A=∠C,可得AD∥CB.
【考点精析】利用平行线的判定对题目进行判断即可得到答案,需要熟知同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:初中数学 来源: 题型:
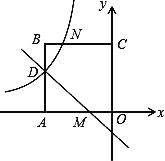
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y =![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.
(1)求反比例函数和一次函数的表达式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
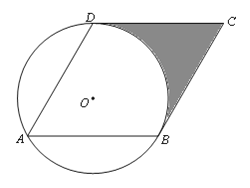
【题目】已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
(1)求证:BC与⊙O相切;
(2)求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】贵阳市某中学开展以“三创一办”为中心,以“校园文明”为主题的手抄报比赛,同学们积极参与,参赛同学每人交了一份得意作品,所有参赛作品均获奖,奖项分为一等奖、二等奖、三等奖和优秀奖,将获奖结果绘制成如下两幅统计图.
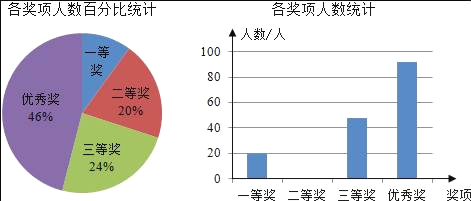
请你根据图中所给信息解答下列问题:
(1)一等奖所占的百分比是 .
(2)在此次比赛中,一共收到多少份参赛作品?请将条形统计图补充完整;
(3)各奖项获奖学生分别有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明袋子中有1个红球、1 个绿球和n个白球,这些球除颜色外都相同.
(1)从袋中随机摸出1个球,记录下颜色后放回袋子中并搅匀,不断重复该试验.发现摸到白球的频率稳定在0.75,则n的值为 ;
(2)当n=2时,把袋中的球搅匀后任意摸出2个球,求摸出的2个球颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B是数轴上的两个点,点A表示的数为13,点B表示的数为-5,动点P从点B出发,以每秒4个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() 秒.
秒.
(1)BP= ,点P表示的数 (分别用含![]() 的代数式表示);
的代数式表示);
(2)点P运动多少秒时,PB=2PA?
(3)若M为BP的中点,N为PA的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com