
【题目】如图,一次函数的图像经过点P(1,3),Q(0,4).

(1)求该函数的表达式;
(2)该图像怎样平移后经过原点?
【答案】(1)y=-x+4;(2)向下平移4个单位长度(或向上平移-4个单位长度);向左平移4个单位长度;或先向左平移1个单位长度,再向下平移3个单位长度;或先向下平移3个单位长度,再向左平移1个单位长度(此问答案不唯一).
【解析】
(1)设y=kx+b(k≠0),直接将P(1,3),Q(0,4)代入,即可用待定系数法求得函数解析式;
(2)平移后经过原点,则平移之后解析式为y=-x,根据函数y=-x+4变形为y=-x的过程,结合函数的平移符合“左加右减,上加下减”即可得出平移方式(答案不唯一).
(1)设y=kx+b(k≠0),
所以![]() ,
,
解得![]()
所以函数表达式为y=-x+4.
(2)若平移后经过原点,则平移后函数的解析式为y=-x.
∵y=-x+4-4=-x,∴可向下平移4个单位长度(或向上平移-4个单位长度);
∵y=-( x+4)+4=- x,∴可向左平移4个单位长度;
∵y=-(x+1)+4-3,∴可先向左平移1个单位长度,再向下平移3个单位长度或先向下平移3个单位长度,再向左平移1个单位长度.


科目:初中数学 来源: 题型:
【题目】小红驾车从甲地到乙地,她出发第xh时距离乙地ykm,已知小红驾车中途休息了1小时,图中的折线表示她在整个驾车过程中y与x之间的函数关系.
(1)B点的坐标为( , );
(2)求线段AB所表示的y与x之间的函数表达式;
(3)小红休息结束后,以60km/h的速度行驶,则点D表示的实际意义是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线l1:y=2x+8与坐标轴分别交于A,B两点,点C在x正半轴上,且OA=OC.点P为线段AC(不含端点)上一动点,将线段OP绕点O逆时针旋转90°,得线段OQ(见图2)
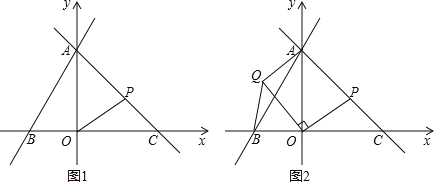
(1)分别求出点B、点C的坐标;
(2)如图2,连接AQ,求证:∠OAQ=45°;
(3)如图2,连接BQ,试求出当线段BQ取得最小值时点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC中,AC=BC=4,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.
(1)当PN∥BC时,判断△ACP的形状,并说明理由;
(2)点P在滑动时,当AP长为多少时,△ADP与△BPC全等,为什么?
(3)点P在滑动时,△PCD的形状可以是等腰三角形吗?若可以,请求出夹角α的大小;若不可以,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买若干台A型电脑和B型打印机.如果购买1台A型电脑,2台B型打印机,一共需要花费5900元;如果购买2台A型电脑,2台B型打印机,一共需要花费9400元.
(1)求每台A型电脑和每台B型打印机的价格分别是多少元?
(2)如果学校购买A型电脑和B型打印机的预算费用不超过20000元,并且购买B型打印机的台数要比购买A型电脑的台数多1台,那么该学校至多能购买多少台B型打印机?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只口袋里放着![]() 个红球、
个红球、![]() 个黑球和若干个白球,这三种球除颜色外没有任何区别,并搅匀.
个黑球和若干个白球,这三种球除颜色外没有任何区别,并搅匀.
![]() 取出红球的概率为
取出红球的概率为![]() ,白球有多少个?
,白球有多少个?
![]() 取出黑球的概率是多少?
取出黑球的概率是多少?
![]() 再在原来的袋中放进多少个红球,能使取出红球的概率达到
再在原来的袋中放进多少个红球,能使取出红球的概率达到![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】飞镖随机地掷在下面的靶子上.
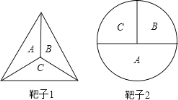
![]() 在每一个靶子中,飞镖投到区域
在每一个靶子中,飞镖投到区域![]() 、
、![]() 、
、![]() 的概率是多少?
的概率是多少?
![]() 在靶子
在靶子![]() 中,飞镖投在区域
中,飞镖投在区域![]() 或
或![]() 中的概率是多少?
中的概率是多少?
![]() 在靶子
在靶子![]() 中,飞镖没有投在区域
中,飞镖没有投在区域![]() 中的概率是多少?
中的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=(2m+4)x,求:
(1)m为何值时,函数图象经过第一、三象限?
(2)m为何值时,y随x的增大而减小?
(3)m为何值时,点(1,3)在该函数的图象上?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com