
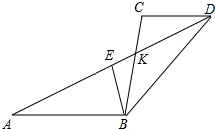
 如图,已知线段AB∥CD,AD与BC相交于点K,∠ABC的角平线分BE交AD于E,当AE=$\frac{1}{2}$AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.
如图,已知线段AB∥CD,AD与BC相交于点K,∠ABC的角平线分BE交AD于E,当AE=$\frac{1}{2}$AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明. 分析 AB=BC+CD.作△ABD的中位线,由中位线定理得EF∥AB∥CD,可知G为BC的中点,由平行线及角平分线性质得∠GEB=∠EBA=∠GBE,则EG=BG=$\frac{1}{2}$BC,而GF=$\frac{1}{2}$CD,EF=$\frac{1}{2}$AB,利用EF=EG+GF求线段AB、BC、CD三者之间的数量关系.
解答 解:猜想:AB=BC+CD,
证明:取BD的中点为F,连接EF交BC于G点,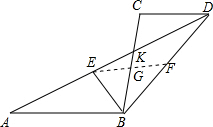 由中位线定理,得EF∥AB∥CD,
由中位线定理,得EF∥AB∥CD,
∴G为BC的中点,∠GEB=∠EBA,
又∵∠EBA=∠GBE,
∴∠GEB=∠GBE,
∴EG=BG=$\frac{1}{2}$BC,而GF=$\frac{1}{2}$CD,EF=$\frac{1}{2}$AB,
∵EF=EG+GF,
即:$\frac{1}{2}$AB=$\frac{1}{2}$BC+$\frac{1}{2}$CD;
∴AB=BC+CD.
点评 本题考查了平行线的性质,三角形中位线定理,角平分线的性质等知识,解题的关键是学会添加常用辅助线,利用三角形中位线定理解决问题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
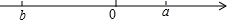 如图,已知数轴上表示数a、b的点:
如图,已知数轴上表示数a、b的点:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2014 | B. | $-\frac{1}{2014}$ | C. | -π | D. | $-\frac{π}{2014}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
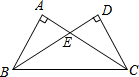 如图,∠A=∠D=90°,要使△ABC≌△DCB,只需要增加:①AB=DC;②AC=DB;③BC=BC;④∠ABC=∠DCB;⑤∠ACB=∠DBC中的一个条件①②④⑤(只需填写一个正确的条件).
如图,∠A=∠D=90°,要使△ABC≌△DCB,只需要增加:①AB=DC;②AC=DB;③BC=BC;④∠ABC=∠DCB;⑤∠ACB=∠DBC中的一个条件①②④⑤(只需填写一个正确的条件).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
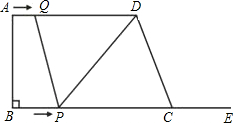 如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).
如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com