
| A. | 30° | B. | 45° | C. | 60° | D. | 70° |
科目:初中数学 来源: 题型:填空题
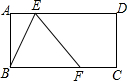 在矩形ABCD中,AB=3,BC=6,将矩形折叠,使B点落在AD(含端点)上,落点记为E,这时折痕与边BC(含端点)交于F,然后展开铺平,则以B、E、F为顶点的△BEF,称为矩形ABCD的“折痕三角形”.当折痕△BEF的面积最大时,AE的长为6-3$\sqrt{3}$.
在矩形ABCD中,AB=3,BC=6,将矩形折叠,使B点落在AD(含端点)上,落点记为E,这时折痕与边BC(含端点)交于F,然后展开铺平,则以B、E、F为顶点的△BEF,称为矩形ABCD的“折痕三角形”.当折痕△BEF的面积最大时,AE的长为6-3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
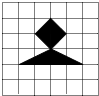 如果小王将镖随意投中如图所示的正方形木板,那么镖落在阴影部分的概率为( )
如果小王将镖随意投中如图所示的正方形木板,那么镖落在阴影部分的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
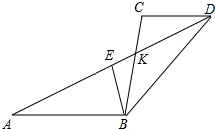 如图,已知线段AB∥CD,AD与BC相交于点K,∠ABC的角平线分BE交AD于E,当AE=$\frac{1}{2}$AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.
如图,已知线段AB∥CD,AD与BC相交于点K,∠ABC的角平线分BE交AD于E,当AE=$\frac{1}{2}$AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
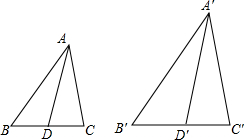 如图,D、D′分别是△ABC和△A′B′C′的边BC、B′C′的中点,且$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$=$\frac{AD}{A′D′}$,求证:△ABC∽△A′B′C′.
如图,D、D′分别是△ABC和△A′B′C′的边BC、B′C′的中点,且$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$=$\frac{AD}{A′D′}$,求证:△ABC∽△A′B′C′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com