
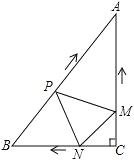
【题目】如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,动点M、N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,MN,设移动时间为t(单位:秒,0<t<2.5).
(1)当时间为t秒时,点P到BC的距离为 cm.
(2)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(3)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .(3) 当t=
.(3) 当t=![]() 时,四边形APNC的面积S有最小值,其最小值是
时,四边形APNC的面积S有最小值,其最小值是![]() .
.
【解析】
试题分析:(1)先根据勾股定理求出AB的长,过点P作PH⊥BC于点H,构造平行线PH∥AC,由平行线分线段成比例求得以t表示的PH的值;
(2)分类讨论:△AMP∽△ABC和△APM∽△ABC两种情况.利用相似三角形的对应边成比例来求t的值;
(3)根据“S=S△ABC-S△BPH”列出S与t的关系式S=![]() (t-
(t-![]() )2+
)2+![]() (0<t<2.5),则由二次函数最值的求法即可得到S的最小值.
(0<t<2.5),则由二次函数最值的求法即可得到S的最小值.
试题解析:(1)∵在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,
∴AB=5cm,
过P作PH⊥BC于H,则∠PHB=∠C=90°,
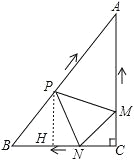
∵∠B=∠B,
∴△BPH∽△BAC,
∴![]()
∴![]() ,
,
解得:PH=![]() (cm),
(cm),
(2)以A,P,M为顶点的三角形与△ABC相似,分两种情况:
①当△AMP∽△ABC时,![]() ,即
,即![]() ,
,
解得t=![]() ;
;
②当△APM∽△ABC时,![]() ,即
,即![]() ,
,
解得t=0(不合题意,舍去);
综上所述,当t=![]() 秒时,以A、P、M为顶点的三角形与△ABC相似;
秒时,以A、P、M为顶点的三角形与△ABC相似;
(3)存在某一时刻t,使四边形APNC的面积S有最小值.理由如下:
假设存在某一时刻t,使四边形APNC的面积S有最小值.
如图,∵由(1)知:PH=![]() ,
,
∴S=S△ABC-S△BPN,
=![]() ×3×4-
×3×4-![]() ×(3-t)t,
×(3-t)t,
=![]() (t-
(t-![]() )2+
)2+![]() (0<t<2.5).
(0<t<2.5).
∵![]() >0,
>0,
∴S有最小值.
当t=![]() 时,S最小值=
时,S最小值=![]() .
.
答:当t=![]() 时,四边形APNC的面积S有最小值,其最小值是
时,四边形APNC的面积S有最小值,其最小值是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】运用交换律和结合律计算:
(1)3-10+7=3________7______10=________;
(2)-6+12-3-5=______6______3______5______12=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )

A. 点C B. 点D C. 点A D. 点B
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期初,我市教育部门对某中学从学生的品德、身心、学习、创新、国际、审美、信息、生活八个方面进行了综合评价,评价小组从八年级学生中选取部分学生针对“信息素养”进行测试,并将测试结果绘制成如下统计图(如图).根据图中信息,解答下列问题:
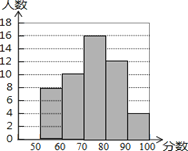
(1)本次选取参加测试的学生人数是 ___;
(2)学生“信息素养”得分的中位数落在 _____;
(3)若把每组中各个分数用这组数据的中间值代替(如30﹣40分的中间值为35分),则参加测试的学
生的平均分为多少分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com