
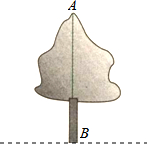
 如图,要测量树AB的高,可以利用相似三角形的知识,请你设计几种测量方案,并说明每种方案的理由.
如图,要测量树AB的高,可以利用相似三角形的知识,请你设计几种测量方案,并说明每种方案的理由. 分析 方案一:利用同一时刻高度与影长的比相等设计;
方案二:利用入射角与反射角相等构造相似三角形,如图2,在距离树AB的地面上E点放一个镜子,人站在镜子的前面F点处能从镜子里看到树的顶点A,这时测出BE=a,EF=b,眼睛到地面的距离为c,然后利用相似比可计算出AB.
解答 解:方案一:如图1,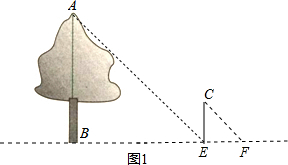
在树AB的影子的BE处直立一根1米长的木杆CE,测出此时树AB的影长BE=a,木杆的影长EF=b,
利用Rt△ABE∽Rt△CEF,则$\frac{AB}{CE}$=$\frac{BE}{EF}$,所以AB=$\frac{a}{b}$;
方案二:如图2,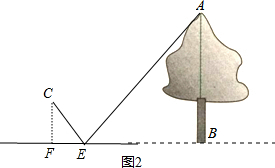
在距离树AB的地面上E点放一个镜子,人站在镜子的前面F点处能从镜子里看到树的顶点A,这时测出BE=a,EF=b,眼睛到地面的距离为c,
由于∠CEF=∠AEB,则Rt△CEF∽Rt△AEB,所以$\frac{EF}{BE}$=$\frac{CF}{AB}$,则AB=$\frac{ac}{b}$.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度;借助标杆或直尺测量物体的高度.


科目:初中数学 来源: 题型:解答题
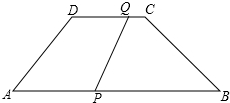 如图,梯形ABCD中,AB∥DC,AD=BC=5cm,AB=12cm,CD=6cm,点Q从C开始沿CD边以1cm/s的速度向D移动,同时点P从A开始沿AB以3cm/s的速度向B移动,当其中一点到达终点时运动停止.设运动时间为t秒.
如图,梯形ABCD中,AB∥DC,AD=BC=5cm,AB=12cm,CD=6cm,点Q从C开始沿CD边以1cm/s的速度向D移动,同时点P从A开始沿AB以3cm/s的速度向B移动,当其中一点到达终点时运动停止.设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
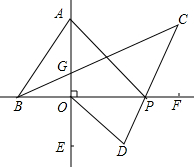 如图,直线AE⊥BF于O,将一个三角板ABO如图放置(∠BAO=30°),两直角边与直线BF,AE重合,P为直线BF上一动点,BC平分∠ABP,PC平分∠APF,OD平分∠POE.
如图,直线AE⊥BF于O,将一个三角板ABO如图放置(∠BAO=30°),两直角边与直线BF,AE重合,P为直线BF上一动点,BC平分∠ABP,PC平分∠APF,OD平分∠POE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com