
����Ŀ�����ǹ涨��һ���ڱ�����ҶԽǻ������ı��ν����������ı�������
��1���ڢ�ƽ���ı��Σ������Σ��۾��Σ����������У�һ��Ϊ���������ı��ε��� ��������ţ���
��2�������������ı���ABCD�У�AB=AD����B+��D=180��������AC��
����ͼ1����֤��ACƽ�֡�BCD��
С��ͨ���۲졢ʵ�飬������������뷨��֤��ACƽ�֡�BCD��
�뷨һ��ͨ����B+��D=180�������ӳ�CB��E��ʹBE=CD��ͨ��֤����AEB�ա�ACD���Ӷ���֤ACƽ�֡�BCD��
�뷨����ͨ��AB=AD���ɽ���ACD�Ƶ�A˳ʱ����ת��ʹAD��AB�غϣ��õ���AEB����֤C,B,E��������ֱ���ϣ��Ӷ���֤ACƽ�֡�BCD.
����ο�������뷨������С��֤��ACƽ�֡�BCD��
����ͼ2������BAD=90�����õ�ʽ��ʾ�߶�AC,BC,CD֮���������ϵ����֤��.


���𰸡���1�������������2���������������BC+CD=![]() AC��
AC��
��������
��1�������������ı������Ķ�������жϳ��������������ı��Σ�
��2�����뷨һ��ͨ����B+��D=180�������ӳ�CB��E��ʹBE=CD��ͨ��֤����AEB�ա�ACD���Ӷ���֤ACƽ�֡�BCD��
�뷨����ͨ��AB=AD���ɽ���ACD�Ƶ�A˳ʱ����ת��ʹAD��AB�غϣ��õ���AEB����֤C,B,E��������ֱ���ϣ��Ӷ���֤ACƽ�֡�BCD��
�ڢ��ӳ�CBʹBE=CD������AE���ɵ���ACEΪ���������Σ���Ϊ��BAD =90���á�EAC=90�����ɹ��ɶ����ɵ�AC,BC,CD֮���������ϵ.
��1����1���������ڵȶԲ��ı������Ķ��壬������һ�������ڵȶԲ��ı�������
�ʴ�Ϊ���ܣ�
��2���뷨һ���ӳ�CBʹBE=CD������AE

�ߡ�ADC+��ABC=180������ABE+��ABC=180����
���ADC=��ABE��
��AD=AB��
���ADC�ա�ABE��
���ACD=��AEB;
AC=AE��
���ACB=��AEB��
���ACD=��ACB��
��ACƽ�֡�BCD
�뷨��������ACD�Ƶ�A˳ʱ����ת��ʹAD����AB���غϣ��õ���ABE��
���ADC�ա�ABE��
���ADC=��ABE;
��ACD=��AEB;
AC=AE��
�ߡ�ADC+��ABC=180����
���ABE+��ABC=180����
���C,B,E��һ��ֱ���ϣ�
��AC=AE��
���ACB=��AEB��
���ACD=��ACB��
��ACƽ�֡�BCD��
���ӳ�CBʹBE=CD������AE��

�ɢٵ���ADC�ա�ABE
��AC=AE
����ACE����������
�ߡ�BAD =90����
���EAC=90����
��![]() ��
��
��![]() ��
��
��BC+CD=![]() AC��
AC��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����һ�ܼƻ�ÿ���������г�100�������ڹ���ʵ�����ݣ�ÿ���ϰ�������һ����ȣ�ʵ��ÿ����������ƻ������������±����Լƻ���Ϊ�������ӵij�������Ϊ���������ٵij�������Ϊ������:
���� | һ | �� | �� | �� | �� | �� | �� |
���������� | ��1 | +3 | ��2 | ��4 | +7 | ��5 | ��10 |
��1������������һ������������ٵ�һ���������������
��2�������ܵ��������Ƕ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������⣺
��1����3������10��+����9����10
��2������1���£�![]() ��
��![]()
��3����![]()
��4����14����1��9����|��4|��[3������3��2]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ij��˾�мס������ྭӪ���룬����ȥ����������Ϊ![]() ��Ԫ��ȥ��������������������2����Ԥ�ƽ���������������9%���������뽫����19%������ù�˾�����������ȥ������__________��Ԫ������ĸ
��Ԫ��ȥ��������������������2����Ԥ�ƽ���������������9%���������뽫����19%������ù�˾�����������ȥ������__________��Ԫ������ĸ![]() ����ʾ����
����ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�����
�У�����![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ���ڵ�A(3,m).
���ڵ�A(3,m).
��1����k��m��ֵ��
��2����֪��P(n��n)(n>0)������P��ƽ����![]() ���ֱ�ߣ���ֱ��y=x-2�ڵ�M������P��ƽ����y���ֱ�ߣ�������
���ֱ�ߣ���ֱ��y=x-2�ڵ�M������P��ƽ����y���ֱ�ߣ�������![]() ��ͼ���ڵ�N.
��ͼ���ڵ�N.
�ٵ�n=1ʱ���ж��߶�PM��PN��������ϵ����˵�����ɣ�
����PN��PM����Ϻ�����ͼ��ֱ��д��n��ȡֵ��Χ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ӹ����֣���֪ÿ1�����ԭ�Ͽ��Լӹ���3��A���ֻ�4��B���֣�˵����ÿ�����ԭ����ͬʱ�ȼӹ�A�����ּ�B���֣�����֪1��A���ֺ�2��B�������һ�������Ϊ�˼ӹ�����������Ҫ��A��B����ǡ�����ף����з��̽���������⣺
��1������25����ͬ�Ľ���ԭ�ϣ�������ܼӹ����ٸ������������
��2������36����ͬ�Ľ���ԭ��ȫ���ӹ��꣬�ʼӹ���A��B����ǡ��������˵������
��3������n����ͬ�Ľ���ԭ��ȫ���ӹ��꣬Ϊ��ʹ�����ӹ�������A��B����ǡ�����ף������n�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�̵���ijһʱ����ÿ��aԪ��a ��0���ļ۸����������·�������һ��ӯ��25%����һ������25%.
��1����a =100ʱ,���������������·��ܵ���ӯ�����ǿ���,���Dz�ӯ������
��2��С�����֣�����aΪ��ֵ�������������·��ܵĶ��ǿ���.���ж���С���������Ƿ���ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����m�ķ���![]() ��m-16��=7�Ľ�Ҳ�ǹ���x�ķ���2��x-3��-n=52�Ľ⣮
��m-16��=7�Ľ�Ҳ�ǹ���x�ķ���2��x-3��-n=52�Ľ⣮
��1����m��n��ֵ��
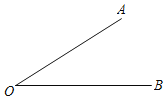
��2����֪��AOB=m������ƽ���ڻ�һ������OP��ǡ��ʹ�á�AOP=n��BOP�����BOP��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���������������ֱ������ĸA��B��C��D��E��F����������ͬ������������ͼ��

��1��A�������ĸ���� ��B�������ĸ���� ��������ֱ����д�𰸣�
��2����֪A��x��B����x2+3x��C����3��D��1��E��x2019��F��6��
������ĸA��ʾ���������������ĸ��ʾ������Ϊ�෴������E��ֵ��
����2A��3B+M��0�����M�ı���ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com