
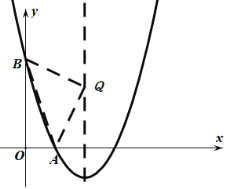
【题目】如图,已知抛物线 ![]() 与
与 ![]() 轴交于A、C两点,与
轴交于A、C两点,与 ![]() 轴交于点B,在抛物线的对称轴上找一点Q,使△ABQ成为等腰三角形,则Q点的坐标是____.
轴交于点B,在抛物线的对称轴上找一点Q,使△ABQ成为等腰三角形,则Q点的坐标是____.
【答案】Q1![]() ,Q2
,Q2![]() ,Q3(2,2),Q4(2,3)
,Q3(2,2),Q4(2,3)
【解析】
先求得点A和点B的坐标,由顶点式知抛物线的对称轴为直线x=2,设抛物线的对称轴上的点Q的坐标为![]() ,分别求得
,分别求得![]() ,并用含
,并用含![]() 的代数式表示
的代数式表示![]() 的长,分
的长,分![]() 三种情况构造方程求得
三种情况构造方程求得![]() 的值.
的值.
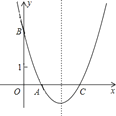
如图,
抛物线的对称轴为直线x=2
当y=0时,
(x-2)2-1=0
解之:x1=3,x2=1
∴点A的坐标为(1,0)
当x=0时,y=3
∴点B(0,3)
设点Q的坐标为(2,m).
∴AB2=32+1=10,BQ2=(m-3)2+22=(m-3)2+4,AQ2=m2+1,
要使△ABQ为等腰三角形,
当AB2=BQ2时,则(m-3)2+4=10,
解之:m1=![]() , m2=
, m2=![]() ,
,
∴点Q1![]() , Q2
, Q2![]() .
.
当BQ2=AQ2时,则(m-3)2+4=m2+1,
解之:m=2
所以点Q2(2,2);
当AB2=AQ2时,则10=m2+1,
解之:m=±3
若m=-3,则点B、A,Q在同一直线上,
∴m=-3舍去,
∴点Q4(2,3)
故答案为:![]() ,Q2
,Q2![]() ,(2,2),(2,3)
,(2,2),(2,3)


科目:初中数学 来源: 题型:
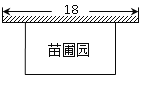
【题目】某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读:
类比是数学中常用的数学思想.比如,我们可以类比多位数的加、减、乘、除的竖式运算方法,得到多项式与多项式的加、减、乘、除的运算方法.

理解应用:
(1)请仿照上面的竖式方法计算:![]() ;
;
(2)已知两个多项式的和为![]() ,其中一个多项式为
,其中一个多项式为![]() .请用竖式的方法求出另一个多项式.
.请用竖式的方法求出另一个多项式.
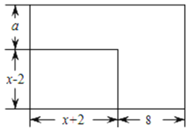
(3)已知一个长为![]() ,宽为
,宽为![]() 的矩形
的矩形![]() ,将它的长增加8.宽增加
,将它的长增加8.宽增加![]() 得到一个新矩形
得到一个新矩形![]() ,且矩形
,且矩形![]() 的周长是
的周长是![]() 周长的3倍(如图).同时,矩形
周长的3倍(如图).同时,矩形![]() 的面积和另一个一边长为
的面积和另一个一边长为![]() 的矩形
的矩形![]() 的面积相等,求
的面积相等,求![]() 的值和矩形
的值和矩形![]() 的另一边长.
的另一边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
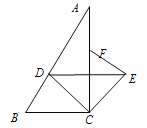
【题目】如图,在△ABC中,![]() ,CD平分
,CD平分![]() 交AB于点D,将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上.
交AB于点D,将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上.
(1)△CDB旋转了________度;
(2)连结DE,判断DE与BC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
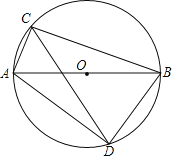
【题目】如图,AB是⊙O的直径,点C,D分别在两个半圆上(不与点A、B重合),AD、BD的长分别是方程x2﹣2![]() x+
x+![]() (m2﹣2m+13)=0的两个实数根.
(m2﹣2m+13)=0的两个实数根.
(1)若∠ADC=15°,求CD的长;
(2)求证:AC+BC=![]() CD.
CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家销售某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x元/件满足一次函数的关系,部分数据如下表:(![]() ,物价部门规定售价不得高于80元)
,物价部门规定售价不得高于80元)
销售单价x(元/件) | … | 55 | 60 | 65 | 70 | 75 |
一周的销售量y(件) | … | 450 | 400 | 350 | 300 | 250 |
(1)直接写出y与x的函数关系式:______;
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并求出销售利润的最大值;
(3)该商家要使每周的销售利润不低于5000元,那么销售单价应控制在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)![]()
(2)![]()
(3)(6x-1)2-25=0
(4)![]()
(5) ![]()
(6) ![]()
(7)![]() +
+![]() +(﹣1)0﹣2sin45°
+(﹣1)0﹣2sin45°
(8)6tan230°-cos30°·tan60°-2sin 45°+cos60°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017甘肃省天水市)△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
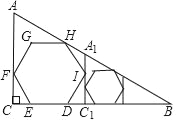
【题目】如图,Rt△ABC中,∠C=Rt∠,AB=2,∠B=30°,正六边形DEFGHI完全落在Rt△ABC内,且DE在BC边上,F在AC边上,H在AB边上,则正六边形DEFGHI的边长为_____,过I作A1C1∥AC,然后在△A1C1B内用同样的方法作第二个正六边形,按照上面的步骤继续下去,则第n个正六边形的边长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com