Question

如图，抛物线y=ax2 + bx + c 交x轴于A、B两点，交y轴于点C，对称轴为直线x=1,已知：A(-1,0)、C(0,-3)。

（1）求抛物线y= ax2 + bx + c 的解析式；

（2）求△AOC和△BOC的面积比；

（3）在对称轴上是否存在一个P点,使△PAC的周长最小。若存在，请你求出点P的坐标；若不存在，请你说明理由。

 

 

Answer 1

（1）y=x2-2x-3．（2）1：3；（3）存在，（1，-2）．

【解析】

试题分析：（1）根据抛物线的对称轴即可得出点B的坐标，然后将A、B、C三点坐标代入抛物线中即可求得二次函数的解析式．

（2）由于两三角形等高，那么面积比就等于底边的比，据此求解即可．

（3）本题的关键是确定P点的位置，根据轴对称图形的性质和两点间线段最短，可找出C点关于抛物线对称轴的对称点，然后连接此点和A，那么这条直线与抛物线对称轴的交点就是所求的P点．可先求出这条直线的解析式然后联立抛物线对称轴的解析式即可求得P点坐标．

试题解析：：（1）∵A，B两点关于x=1对称，

∴B点坐标为（3，0），

根据题意得：

，

解得a=1，b=-2，c=-3．

∴抛物线的解析式为y=x2-2x-3．

（2）△AOC和△BOC的面积分别为S△AOC=1 2 |OA|•|OC|，S△BOC=1 2 |OB|•|OC|，

而|OA|=1，|OB|=3，

∴S△AOC：S△BOC=|OA|：|OB|=1：3．

（3）存在一个点P．C点关于x=1对称点坐标C'为（2，-3），

令直线AC'的解析式为y=kx+b

∴，

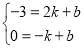∴k=-1，b=-1，即AC'的解析式为y=-x-1．

为x=1时，y=-2，

∴P点坐标为（1，-2）．

考点：二次函数综合题．