
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=9cm,DE=3cm,则BC=12cm.
如图,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=9cm,DE=3cm,则BC=12cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
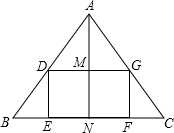 如图,在△ABC中,AB=AC=10,BC=12,矩形DEFG的顶点位于△ABC的边上,设EF=x,SDEFG=y.
如图,在△ABC中,AB=AC=10,BC=12,矩形DEFG的顶点位于△ABC的边上,设EF=x,SDEFG=y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
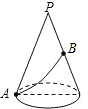 如图,一个圆锥的母线长为10cm,底面半径为5cm,在圆锥的底面边缘上一点A处有一只蚂蚁,想吃到点A相对的母线的中点B处的一粒砂糖,这只蚂蚁从点A出发,沿着曲面爬到点B,最短路线的长是多少?
如图,一个圆锥的母线长为10cm,底面半径为5cm,在圆锥的底面边缘上一点A处有一只蚂蚁,想吃到点A相对的母线的中点B处的一粒砂糖,这只蚂蚁从点A出发,沿着曲面爬到点B,最短路线的长是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
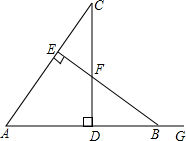 如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB延长线上一点.
如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB延长线上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com