
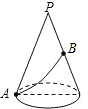
 如图,一个圆锥的母线长为10cm,底面半径为5cm,在圆锥的底面边缘上一点A处有一只蚂蚁,想吃到点A相对的母线的中点B处的一粒砂糖,这只蚂蚁从点A出发,沿着曲面爬到点B,最短路线的长是多少?
如图,一个圆锥的母线长为10cm,底面半径为5cm,在圆锥的底面边缘上一点A处有一只蚂蚁,想吃到点A相对的母线的中点B处的一粒砂糖,这只蚂蚁从点A出发,沿着曲面爬到点B,最短路线的长是多少? 分析 将圆锥侧面展开,进而根据平面上两点之间的距离,线段最短,求出最短路程.
解答 解:∵一个圆锥的母线长为10cm,底面半径为5cm,
故圆锥侧面展开图的圆心角α满足:$\frac{α}{360°}=\frac{5}{10}=\frac{1}{2}$,
故α=180°,
如下图所示: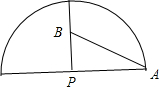
则AB的长度即为所求最短路程,
连接AB,可得△PAB为边长为直角三角形,
故AB=$\sqrt{A{P}^{2}+P{B}^{2}}=\sqrt{1{0}^{2}+{5}^{2}}=5\sqrt{5}$cm,
故从点A出发在侧面上运动到点B的最短路程为5$\sqrt{5}$cm.
点评 考查圆锥侧面展开图中两点间距离的求法;把立体几何转化为平面几何来求是解决本题的突破点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
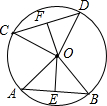 如图,在⊙O中,AB与CD是两条弦,OE⊥AB,OF⊥CD,垂足分别是点E,F,OE,OF分别叫做弦AB,CD的弦心距.
如图,在⊙O中,AB与CD是两条弦,OE⊥AB,OF⊥CD,垂足分别是点E,F,OE,OF分别叫做弦AB,CD的弦心距.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com