练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．先化简，再求值：
    （1）（x+y）2-4xy，其中x=12，y=9．
    （2）（2a+b）（2a-b）+b（2a+b）-4a2，其中a=-$\frac{1}{2}$，b=2．

    分析 （1）利用完全平方公式计算和因式分解，进一步代入求得答案即可；
    （2）利用整式的乘法和平方差公式计算，进一步代入求得答案即可．

    解答 解：（1）原式=x2+2xy+y2-4xy
    =（x-y）2，
    当x=12，y=9时，
    原式=9．
    （2）原式=4a2-b2+2ab+b2-4a2
    =2ab，
    当a=-$\frac{1}{2}$，b=2时，
    原式=-2．

    点评 此题考查整式的化简求值，先利用整式的乘法计算公式和计算方法计算合并，进一步代入求得答案即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

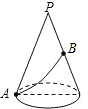    7．如图，一个圆锥的母线长为10cm，底面半径为5cm，在圆锥的底面边缘上一点A处有一只蚂蚁，想吃到点A相对的母线的中点B处的一粒砂糖，这只蚂蚁从点A出发，沿着曲面爬到点B，最短路线的长是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．解下列方程组：
    （1）$\left\{\begin{array}{l}{x-2y=5}\\{2x+7y=-1}\end{array}\right.$
    （2）$\left\{\begin{array}{l}{5（x-9）=6（y-2）}\\{\frac{x}{4}-\frac{y+1}{3}=2}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：
    （1）$\frac{1}{\sqrt{3}}$+3$\sqrt{12}$-$\sqrt{48}$；
    （2）$\sqrt{\frac{1}{6}}$×$\sqrt{8}$×$\sqrt{27}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

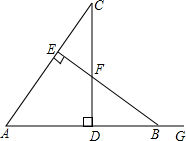    12．如图，CD⊥AB于点D，BE⊥AC于点E，△ABE≌△ACD，∠C=42°，AB=9，AD=6，G为AB延长线上一点．
    （1）求∠EBG的度数．
    （2）求CE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．若点P（2a+1，1-a）在第二象限，则a的取值范围是a＜-$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．甲市欲将一批水果运往乙市销售，现有火车、汽车两种运输方式，这两种运输方式的所需费用如下表（途中费用是指每公里所需的运输费用）：
    运输工具途中费用（元/km）装卸总费用（元）
    火车42000
    汽车81000
    设甲、乙两市间的距离为xkm，
    （1）如果用y1，y2分别表示使用火车、汽车运输时的总支出费用，分别写出y1，y2与x间的表达式；
    （2）当x=300时，应采用哪种运输方式，才能使运输时的总支出费用最小？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．如果函数y=x-b与y=-2x+4的图象的交点坐标是（2，0），那么二元一次方程组$\left\{\begin{array}{l}{x-y=b}\\{2x+y=4}\end{array}\right.$的解是（　　）
    A．（2，0）B．$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$C．$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$D．以上答案都不对

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知Rt△ABC≌Rt△DBE，∠ACB=∠DEB=90°，∠A=∠D．
    （1）将两三角形按图①方式摆放，其中点E落在AB上，DE所在直线交边AC于点F．求证：AF+EF=DE；
    （2）若将两三角形按照图②方式摆放，边AC的延长线与DE相交于点F．你认为（1）中的结论还成立吗？若成立，写出证明过程；若不成立，请写出AF、EF与DE之间的关系，并说明理由．

    查看答案和解析>>

    同步练习册答案