
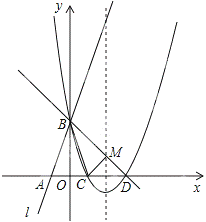
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
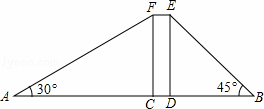
宾哥和君哥在华润广场前感慨楼房真高.君哥说:“这楼起码20层!”宾哥却不以为然:“20层?我看没有,数数就知道了!”君哥说:“老大,你有办法不用数就知道吗?”宾哥想了想说:“没问题!让我们来量一量吧!”君哥、宾哥在楼体两侧各选A、B两点,其中矩形CDEF表示楼体,AB=200米,CD=20米,∠A=30°,∠B=45°,(A、C、D、B四点在同一直线上)问:
(1)楼高多少米?(用含根号的式子表示)
(2)若每层楼按3米计算,你支持宾哥还是君哥的观点呢?请说明理由.(精确到0.1,参考数据: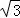 ≈1.73,
≈1.73,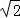 ≈1.41,
≈1.41,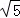 ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
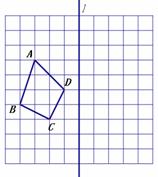
如图,在边长为1的小正方形组成的10×10网格中(我们把组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A、B、C、D分别在网格的格点上.
(1)请你在所给的网格中画出四边形A′B′C′D′,使四边形A′B′C′D′和四边形ABCD关于直线l对称,其中点A′、B′、C′、D′分别是点A、B、C、D的对称点;
(2)在(1)的条件下,结合你所画的图形,直接写出线段A′B′的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
在△ABC中,BD,CE是它的两条角平分线,且BD,CE相交于点M,MN⊥BC于点N.将∠MBN记为∠1,∠MCN记为∠2,∠CMN记为∠3.
(1)(4分)如图1,若∠A=110°,∠BEC=130°,则∠2= °,∠3-∠1= °;
(2)(4分)如图2,猜想∠3-∠1与∠A的数量关系,并证明你的 结论;
结论;
(3)(4分)若∠BEC=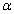 ,∠BDC=
,∠BDC=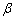 ,用含
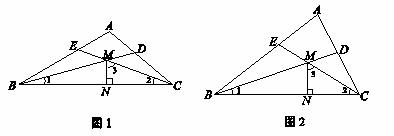
,用含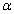 和
和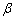 的代数式表示∠3-∠1的度数.(直接写出结果即可)
的代数式表示∠3-∠1的度数.(直接写出结果即可)
解:(2)∠3-∠1与∠A的数量关系是: .
证明:
(3)∠3-∠1= .
查看答案和解析>>
科目:初中数学 来源: 题型:
如果10 =n,那么称b为n的“拉格数”,记为d (n),由定义可知:d (n)=b.如
=n,那么称b为n的“拉格数”,记为d (n),由定义可知:d (n)=b.如 ,
,
则d (100)= d ( )=2,给出下列关于“拉格数”d (n)的结论:①d(10)=10,②d(10
)=2,给出下列关于“拉格数”d (n)的结论:①d(10)=10,②d(10 )=-2,
)=-2,
③ =3,④d(mn) =d(m)+d(n),⑤d(
=3,④d(mn) =d(m)+d(n),⑤d( )=d(m)÷d(n).
)=d(m)÷d(n).
其中,正确的结论有(填写所有正确的序号)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com