
【题目】如图,在数轴上点A表示数a,点B表示数b,AB表示A点和B点之间的距离,且a,b满足|a+2|+(b+3a)2=0.
(1)求A,B两点之间的距离;
(2)若在线段AB上存在一点C,且AC=2BC,求C点表示的数;
(3)若在原点O处放一个挡板,一小球甲从点A处以1个单位/秒的速度向左运动,同时,另一个小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略小球的大小,可看做一个点)以原来的速度向相反的方向运动.
设运动时间为t秒.
①甲球到原点的距离为_____,乙球到原点的距离为_________;(用含t的代数式表示)
②求甲乙两小球到原点距离相等时经历的时间.
![]()
【答案】 2+t 6-2t或2t-6
【解析】(1)、先根据非负数的性质求出a、b的值,再根据两点间的距离公式即可求得A、B两点之间的距离;(2)、设BC的长为x,则AC=2x,根据AB的长度得出x的值,从而得出点C所表示的数;(3)①甲球到原点的距离=甲球运动的路程+OA的长,乙球到原点的距离分两种情况:(Ⅰ)当0<t≤3时,乙球从点B处开始向左运动,一直到原点O,此时OB的长度-乙球运动的路程即为乙球到原点的距离;(Ⅱ)当t>3时,乙球从原点O处开始向右运动,此时乙球运动的路程-OB的长度即为乙球到原点的距离;②分两种情况:(Ⅰ)0<t≤3,(Ⅱ)t>3,根据甲、乙两小球到原点的距离相等列出关于t的方程,解方程即可.
(1)、由题意知a=-2,b=6,故AB=8.
(2)、设BC的长为x,则AC=2x, ∵BC+AC=AB,∴x+2x=8,解得x=![]() , ∴C点表示的数为6-
, ∴C点表示的数为6-![]() =
=![]() .
.
(3)①2+t;6-2t或2t-6.
②当2+t=6-2t时,解得t=![]() , 当2+t=2t-6时, 解得t=8. ∴t=
, 当2+t=2t-6时, 解得t=8. ∴t=![]() 或8.
或8.


科目:初中数学 来源: 题型:
【题目】应用题
有A、B两个商场以同样价格出售同样商品,且各自推出了不同的优惠方案:
在A商场累计购物超过200元后,超出部分按80%收费;
在B商场累计购物满100元后,超出的部分按90%收费。
设累计购物x(x>200)元,用x表示A、B两商场的实际费用并指明顾客选择到哪家购物合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:

对这两名运动员的成绩进行比较,下列四个结论中,不正确的是( )
A. 甲运动员得分的极差大于乙运动员得分的极差
B. 甲运动员得分的中位数大于乙运动员得分的中位数
C. 甲运动员得分的平均数大于乙运动员得分的平均数
D. 甲运动员的成绩比乙运动员的成绩稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)计算两队决赛成绩的平均数;
(2)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E在边BC上,如果点F是边AD上的点,那么△CDF与△ABE不一定全等的条件是( )
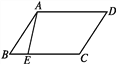
A. DF=BE B. AF=CE
C. CF=AE D. CF∥AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度是( )
A. 第一次向右拐40, 第二次向左拐140
B. 第一次向左拐40, 第二次向右拐40
C. 第一次向左拐40, 第二次向左拐140
D. 第一次向右拐40, 第二次向右拐40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图(1),已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.

(1)试说明OE=OF;
(2)如图(2),若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出说明理由;如果不成立,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com