
【题目】(10分)如图(1),已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.

(1)试说明OE=OF;
(2)如图(2),若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出说明理由;如果不成立,请说明理由.

【答案】详见解析.
【解析】
试题分析:(1)根据正方形的性质对角线垂直且平分,得到OB=OA,又因为AM⊥BE,所以∠MEA+∠MAE=90°=∠AFO+∠MAE,从而求证出Rt△BOE≌Rt△AOF,得到OE=OF.(2)根据第一步得到的结果以及正方形的性质得到OB=OA,再根据已知条件求证出Rt△BOE≌Rt△AOF,得到OE=OF.
试题解析:(1)证明:∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠MEA=∠AFO.
∴Rt△BOE≌Rt△AOF.
∴OE=OF.
解:OE=OF成立.
证明:∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠F+∠MBF=90°,
∠E+∠OBE=90°,
又∵∠MBF=∠OBE,
∴∠F=∠E.
∴Rt△BOE≌Rt△AOF.
∴OE=OF.


科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示数a,点B表示数b,AB表示A点和B点之间的距离,且a,b满足|a+2|+(b+3a)2=0.
(1)求A,B两点之间的距离;
(2)若在线段AB上存在一点C,且AC=2BC,求C点表示的数;
(3)若在原点O处放一个挡板,一小球甲从点A处以1个单位/秒的速度向左运动,同时,另一个小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略小球的大小,可看做一个点)以原来的速度向相反的方向运动.
设运动时间为t秒.
①甲球到原点的距离为_____,乙球到原点的距离为_________;(用含t的代数式表示)
②求甲乙两小球到原点距离相等时经历的时间.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当前正值草莓销售季节,小李用2000元在安塞区草莓基地购进草莓若干进行销售,由于销售状况良好,他又拿出6000元资金购进该种草莓,但这次的进货价比第一次的进货价提高了20%,购进草莓数量比第一次的2倍还多20千克。求该种草莓第一次进价是每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年是一个让人记忆犹新的年份,雾霾天气持续笼罩我国大部分地区,口罩市场出现热销,某旗舰网店用8000元购进甲、乙两种型号的口罩,销售完后共获利2800元,进价和售价如下表:
品名 价格 | 甲型口罩 | 乙型口罩 |
进价(元/袋) | 20 | 25 |
售价(元/袋) | 26 | 35 |
(1)求该网店购进甲、乙两种型号口罩各多少袋?
(2)该网店第二次以原价购进甲、乙两种型号口罩,购进乙种型号口罩袋数不变,而购进甲种型号口罩袋数是第一次的2倍.甲种口罩按原售价出售,而乙种口罩让利销售.若两种型号的口罩都售完,要使第二次销售活动获利不少于3680元,乙种型号的口罩最低售价为每袋多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF. 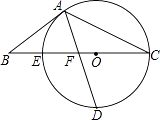
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF= ![]() ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于点E,BF平分∠ABC,交CD于点F.
(1)、求证:DE=BF;(2)、连接EF,写出图中所有的全等三角形.(不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如表:
选手 | 选拔成绩/环 | 中位数 | 平均数 | |||||
甲 | 10 | 9 | 8 | 8 | 10 | 9 | ||
乙 | 10 | 10 | 8 | 10 | 7 | 9 | ||
(1)把表中所空各项数据填写完整;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1),(2)计算的结果,你认为推荐谁参加省比赛更合适?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DCE均是等腰三角形,CA=CB,CD=CE,∠BCA=∠DCE.

(1)求证:BD=AE;
(2)若∠BAC=70°,求∠BPE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com