
【题目】市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如表:
选手 | 选拔成绩/环 | 中位数 | 平均数 | |||||
甲 | 10 | 9 | 8 | 8 | 10 | 9 | ||
乙 | 10 | 10 | 8 | 10 | 7 | 9 | ||
(1)把表中所空各项数据填写完整;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1),(2)计算的结果,你认为推荐谁参加省比赛更合适?请说明理由.
【答案】(1)甲:为9.乙:为9, 9,9,9,9.5;(2)甲: ![]() ,乙:
,乙: ![]() ;(3)甲参加比赛更合适.理由略.
;(3)甲参加比赛更合适.理由略.
【解析】试题分析:(1)根据平均数、中位数的定义,结合图表数据,即可完成表格;
(2)根据平均数,以及方差公式求出甲、乙六次测试成绩的方差即可;
(3)根据方差和平均数两者进行分析.
试题解析:
(1)甲:将六次测试成绩按从小到大的顺序排列为:8,8,9,9,10,10,中位数为(9+9)÷2=9,
平均数为(10+9+8+8+10+9)÷6=9;
乙:第6次成绩为9×6-(10+10+8+10+7)=9,
将六次测试成绩按从小到大的顺序排列为:7,8,9,10,10,10,中位数为(9+10)÷2=9.5;
填表如下:

故答案为9,9.9,9.5
(2)s2甲=![]() [2×(8-9)2+2×(9-9)2+2×(10-9)2]=
[2×(8-9)2+2×(9-9)2+2×(10-9)2]= ![]() ;
;
s2乙=![]() [(7-9)2+(8-9)2+(9-9)2+3×(10-9)2]=
[(7-9)2+(8-9)2+(9-9)2+3×(10-9)2]= ![]() ;
;
(3)我认为推荐甲参加全国比赛更合适,理由如下:
两人的平均成绩相等,说明实力相当;但甲的六次测试成绩的方差比乙小,说明甲发挥较为稳定,故推荐甲参加比赛更合适.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度是( )
A. 第一次向右拐40, 第二次向左拐140
B. 第一次向左拐40, 第二次向右拐40
C. 第一次向左拐40, 第二次向左拐140
D. 第一次向右拐40, 第二次向右拐40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图(1),已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.

(1)试说明OE=OF;
(2)如图(2),若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出说明理由;如果不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与直线y= ![]() x﹣3交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
x﹣3交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.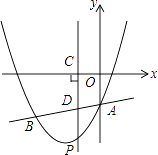
(1)求抛物线的解析式;
(2)以O,A,P,D为顶点的平行四边形是否存在?如存在,求点P的坐标;若不存在,说明理由.
(3)当点P运动到直线AB下方某一处时,过点P作PM⊥AB,垂足为M,连接PA使△PAM为等腰直角三角形,请直接写出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学的五次数学测验成绩如下:
甲 | 81 | 98 | 76 | 95 | 100 |
乙 | 86 | 88 | 91 | 93 | 92 |
如果这个班数学成绩的平均数为75分,试根据以上数据,对甲、乙两名学生的数学学习状况作出分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板按如图所示叠放在一起,若固定![]() ,将
,将![]() 绕着公共顶点
绕着公共顶点![]() ,按顺时针方向旋转
,按顺时针方向旋转![]() 度
度![]() ,当
,当![]() 的一边与
的一边与![]() 的某一边平行时,相应的旋转角
的某一边平行时,相应的旋转角![]() 的度数为_________________。
的度数为_________________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C,且B(1,0),C(0,3),将△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.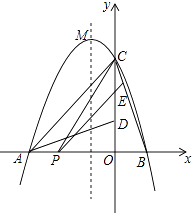
(1)求该二次函数的解析式;
(2)若点P为线段AB上的任一动点,过点P作PE∥AC,交BC于点E,连结CP,求△PCE面积S的最大值;
(3)设抛物线的顶点为M,Q为它的图象上的任一动点,若△OMQ为以OM为底的等腰三角形,求Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com