
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.

【答案】(1)证明见解析;(2)AB+AC=2AE.
【解析】试题分析:(1)根据相“HL”定理得出△BDE≌△CDF,故可得出DE=DF,根据角平分线的判定可得AD平分∠BAC;
(2)BE=CF,AD平分∠BAC,故可得出△AED≌△AFD,所以AE=AF,故AB+AC=AE-BE+AF+CF=AE+AE=2AE.
试题解析:
解:(1)∵DE⊥AB于E,DF⊥AC于F,
∴∠E=∠DFC=90°,
∴△BDE与△CDE均为直角三角形,
∵![]() ,
,
∴△BDE≌△CDF,
∴DE=DF,
∵DE⊥AB于E,DF⊥AC于F,
∴AD平分∠BAC;
(2)AB+AC=2AE.
理由:∵BE=CF,AD平分∠BAC,
∴∠EAD=∠CAD,
∵∠E=∠AFD=90°,
∴∠ADE=∠ADF,
在△AED与△AFD中,
∵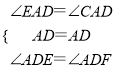 ,
,
∴△AED≌△AFD,
∴AE=AF,
∴AB+AC=AE-BE+AF+CF=AE+AE=2AE.


科目:初中数学 来源: 题型:
【题目】市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如表:
选手 | 选拔成绩/环 | 中位数 | 平均数 | |||||
甲 | 10 | 9 | 8 | 8 | 10 | 9 | ||
乙 | 10 | 10 | 8 | 10 | 7 | 9 | ||
(1)把表中所空各项数据填写完整;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1),(2)计算的结果,你认为推荐谁参加省比赛更合适?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DCE均是等腰三角形,CA=CB,CD=CE,∠BCA=∠DCE.

(1)求证:BD=AE;
(2)若∠BAC=70°,求∠BPE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
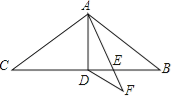
【题目】如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
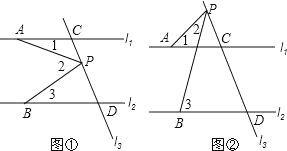
【题目】已知直线 l1∥l2,l3 和 l1,l2 分别交于 C,D 两点,点 A,B 分别在线 l1,l2 上,且位于 l3 的左 侧,点 P 在直线 l3 上,且不和点 C,D 重合.
(1)如图 1,有一动点 P 在线段 CD 之间运动时,试确定∠1、∠2、∠3 之间的关系,并给出证明;
(2)如图 2,当动点 P 在线段 CD 之外运动时,上述的结论是否成立?若不成立,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:
类别 彩电 冰箱 洗衣机
进价(元/台) 2000 1600 1000
售价(元/台) 2300 1800 1100
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.
(1)商店至多可以购买冰箱多少台?
(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
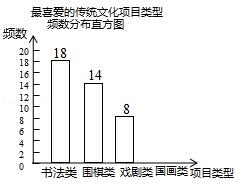
【题目】某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图. 最喜爱的传统文化项目类型频数分布表
项目类型 | 频数 | 频率 |
书法类 | 18 | a |
围棋类 | 14 | 0.28 |
喜剧类 | 8 | 0.16 |
国画类 | b | 0.20 |
根据以上信息完成下列问题:
(1)频数分布表中a= , b=;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
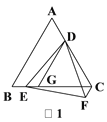
【题目】如图,△ABC是等边三角形,点D在边AC上(点D不与点A,C重合),点E是射线BC上的一个动点(点E不与点B,C重合),连接DE,以DE为边作等边△DEF,连接CF.
(1)如图1,当DE的延长线与AB的延长线相交,且点C,F在直线DE的同侧时,过点D作DG∥AB,DG交BC于点G,求证:CF=EG;
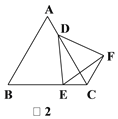
(2)如图2,当DE的反向延长线与AB的反向延长线相交,且点C,F在直线DE的同侧时,求证:CD=CE+CF;
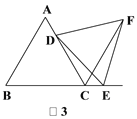
(3)如图3,当DE的反向延长线与线段AB相交,且点C,F在直线DE的异侧时,猜想CD、CE、CF之间的等量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com