
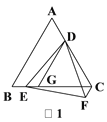
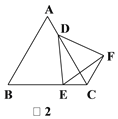
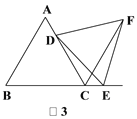
【题目】如图,△ABC是等边三角形,点D在边AC上(点D不与点A,C重合),点E是射线BC上的一个动点(点E不与点B,C重合),连接DE,以DE为边作等边△DEF,连接CF.
(1)如图1,当DE的延长线与AB的延长线相交,且点C,F在直线DE的同侧时,过点D作DG∥AB,DG交BC于点G,求证:CF=EG;
(2)如图2,当DE的反向延长线与AB的反向延长线相交,且点C,F在直线DE的同侧时,求证:CD=CE+CF;
(3)如图3,当DE的反向延长线与线段AB相交,且点C,F在直线DE的异侧时,猜想CD、CE、CF之间的等量关系,并说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)FC=DC+EC,证明见解析.
【解析】试题分析:(1)根据等边三角形的性质和平行线的性质证出△DCG是等边三角形,得出DC=DG,由△DEF是等边三角形得出DF=DE,然后根据角的关系得出∠EDG=∠FDC,进而得出△EDG≌△FDC,根据全等三角形的性质即可得出结论;
(2)过点D作DG∥AB,DG交BC于点G.同(1)的证明思路可得△EDG≌△FDC.根据全等三角形的对应边相等等量代换即可得出结论;
(3)过点D作DG∥AB,DG交BC于点G.类似于(1)(2)的证明思路可得△EDG≌△FDC.根据全等三角形的对应边相等等量代换即可得出结论.
试题解析:
(1)证明:如图1,∵△ABC是等边三角形,
∴∠B=∠ACB=60°.
∵DG∥AB,
∴∠DGC=∠B.

∴∠DGC=∠DCG=60°.
∴△DGC是等边三角形.
∴DC=DG,∠CDG=60°,
∵△DEF是等边三角形,
∴DE=DF,∠EDF=60°
∴∠EDG=60°-∠GDF,∠FDC=60°-∠GDF,
∴∠EDG=∠FDC,
∴△EDG≌△FDC.
∴FC=EG.
(2)证明:∵△ABC是等边三角形,
∴∠B=∠ACB=60°.
如图2,过点D作DG∥AB,DG交BC于点G.

∴∠DGC=∠B=60°.
∴∠DGC=∠DCG=60°
∴△DGC是等边三角形.
∴CD=DG=CG,∠CDG=60°,
∵△DEF是等边三角形,
∴DE=DF,∠EDF=60°,
∴∠EDG=60°-∠CDE,∠FDC=60°-∠CDE,
∴∠EDG=∠FDC.
∴△EDG≌△FDC.
∴EG=FC.
∵CG=CE+EG,
∴CG=CE+FC.
∴CD=CE+FC.
(3)解:如图3,猜想DC、EC、FC之间的等量关系是FC=DC+EC.
证明如下:
∵△ABC是等边三角形,
∴∠B=∠ACB=60°.
过点D作DG∥AB,DG交BC于点G.

∴∠DGC=∠B.
∴∠DGC=∠DCG=60°
∴△DGC是等边三角形.
∴CD=DG=CG,∠CDG=60°.
∵△DEF是等边三角形,
∴DE=DF,∠EDF=60°,
∴∠EDG=60°+∠CDE,∠FDC=60°+∠CDE,
∴∠EDG=∠FDC.
∴△EDG≌△FDC.
∴EG=FC.
∵EG=EC+CG,
∴FC=EC+DC.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=x﹣ ![]() 与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y=
与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y= ![]() x2+bx+c经过点B(﹣1,0)和点C.
x2+bx+c经过点B(﹣1,0)和点C.
(1)填空:直接写出抛物线的解析式:;
(2)已知点Q是抛物线y= ![]() x2+bx+c在第四象限内的一个动点.
x2+bx+c在第四象限内的一个动点.
①如图,连接AQ、CQ,设点Q的横坐标为t,△AQC的面积为S,求S与t的函数关系式,并求出S的最大值;
②连接BQ交AC于点D,连接BC,以BD为直径作⊙I,分别交BC、AB于点E、F,连接EF,求线段EF的最小值,并直接写出此时Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对“共享单车”的使用情况,随机抽取部分学生进行问卷调查,将这次调查的结果绘制了以下两幅不完整的统计图.
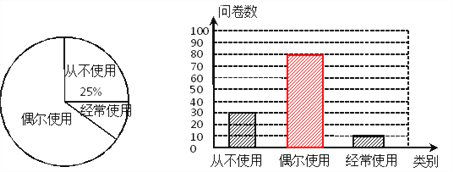
根据以上信息解答下列问题:
(1)本次抽样调查了 学生,“经常使用”部分对应扇形的圆心角度数为 ;
(2)把条形统计图补充完整;
(3)已知全校共3000名学生,请估计经常使用“共享单车”的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我区的葡萄喜获丰收,葡萄一上市,水果店的王老板用2400元购进一批葡萄,很快售完;老板又用5000元购进第二批葡萄,所购件数是第一批的2倍,但进价比第一批每件多了5元.
(1)第一批葡萄每件进价多少元?
(2)王老板以每件150元的价格销售第二批葡萄,售出80%后,为了尽快售完,决定打折促销,要使第二批葡萄的销售利润不少于640元,剩余的葡萄每件售价最少打几折?(利润=售价-进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2﹣5ax+4a与x轴交于A、B(A点在B点的左侧)与y轴交于点C.
(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;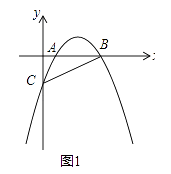
(2)如图2,点P为第四象限抛物线上一点,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;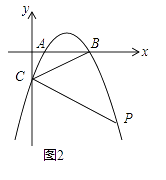
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4 ![]() a,连接KB并延长交抛物线于点Q,求PQ的长.
a,连接KB并延长交抛物线于点Q,求PQ的长.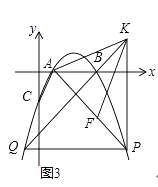
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=4,以顶点A,B为圆心,以AD、BC长为半径作两条弧,两弧相切于点E,且E在AB上,以AB为直径作半圆恰好与DC相切,则图中阴影部分的面积为 . 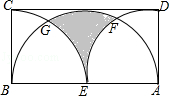
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长江是我们的母亲河,金港新区为了打造沿江风景,吸引游客搞活经济,将一段长为180米的沿江河道整治任务交由A、B两工程队先后接力完成.A工作队每天整治12米,B工程队每天整治8米,共用时20天.求A、B两工程队分别整治河道多少米?
⑴根据题意,七⑴班甲同学列出尚不完整的方程组如下。根据甲同学所列的方程组,请你分别指出未知数x、y表示的意义,然后在方框中补全甲同学所列的方程组;
![]() ,x表示________________________,y表示_________________________;
,x表示________________________,y表示_________________________;
⑵如果乙同学直接设A工程队整治河道的米数为x,B工程队整治河道的米数为y,列出了一个方程组,求A、B两工程队分别整治河道多少米.请你帮助他写出完整的解答过程。
查看答案和解析>>
科目:初中数学 来源: 题型:
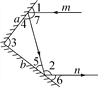
【题目】实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射.若被b反射出的光线n与光线m平行,且∠1=50°,则∠2=________,∠3=________;
(2)在(1)中,若∠1=55°,则∠3=________;若∠1=40°,则∠3=________;
(3)由(1)、(2)请你猜想:当两平面镜a,b的夹角∠3=________时,可以使任何射到平面镜a上的光线m,经过平面镜a,b的两次反射后,入射光线m与反射光线n平行,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com