
【题目】如图,△ABC和△DCE均是等腰三角形,CA=CB,CD=CE,∠BCA=∠DCE.

(1)求证:BD=AE;
(2)若∠BAC=70°,求∠BPE的度数.
【答案】(1)见解析;(2)140°
【解析】试题分析:(1)由CA=CB,CD=CE,∠ACB=∠DCE=α,利用SAS即可判定△ACD≌△BCE;
(2)根据△ACD≌△BCE,得出∠CBD=∠CAE,再根据∠APC=∠ACB,即可解决问题.
试题解析:(1)证明:∵∠BCA=∠DCE
∴∠BCA+∠ACD=∠DCE+∠ACD 即∠BCD=∠ACE
在 △BCD和△ACE中,
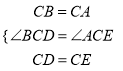
∴△BCD≌△ACE
∴BD=AE
(2)解:∵CA=CB
∴∠CBA=∠CAB=70°
由(1)得:△BCD≌△ACE
∴∠EAC=∠DBC
∴∠BPE=∠BAP+∠ABD=(∠BAC+∠CAE)+∠ABP
=∠BAC+(∠CBD+∠ABP)=∠BAC+∠ABC=140°


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
【题目】(10分)如图(1),已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.

(1)试说明OE=OF;
(2)如图(2),若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出说明理由;如果不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C,且B(1,0),C(0,3),将△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.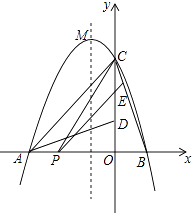
(1)求该二次函数的解析式;
(2)若点P为线段AB上的任一动点,过点P作PE∥AC,交BC于点E,连结CP,求△PCE面积S的最大值;
(3)设抛物线的顶点为M,Q为它的图象上的任一动点,若△OMQ为以OM为底的等腰三角形,求Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班所有学生参加2010年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:

(1)九年级(1)班参加体育测试的学生有 人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,等级B部分所占的百分比是 ,等级C对应的圆心角的度数为 ;
(4)若该校九年级学生共有850人参加体育测试,估计达到A级和B级的学生共有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为( )

A. 115° B. 120° C. 125° D. 130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=x﹣ ![]() 与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y=
与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y= ![]() x2+bx+c经过点B(﹣1,0)和点C.
x2+bx+c经过点B(﹣1,0)和点C.
(1)填空:直接写出抛物线的解析式:;
(2)已知点Q是抛物线y= ![]() x2+bx+c在第四象限内的一个动点.
x2+bx+c在第四象限内的一个动点.
①如图,连接AQ、CQ,设点Q的横坐标为t,△AQC的面积为S,求S与t的函数关系式,并求出S的最大值;
②连接BQ交AC于点D,连接BC,以BD为直径作⊙I,分别交BC、AB于点E、F,连接EF,求线段EF的最小值,并直接写出此时Q点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com