练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图是由射线AB，BC，CD，DE，EA组成的平面图形，则∠1+∠2+∠3+∠4+∠5= ．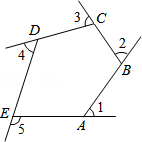

    【答案】360°
    【解析】解：∠1+∠2+∠3+∠4+∠5 =（180°﹣∠BAE）+（180°﹣∠ABC）+（180°﹣∠BCD）+（180°﹣∠CDE）+（180°﹣∠DEA）
    =180°×5﹣（∠BAE+∠ABC+∠BCD+∠CDE+∠DEA）
    =900°﹣（5﹣2）×180°
    =900°﹣540°
    =360°．
    故答案为：360°．
    首先根据图示，可得∠1=180°﹣∠BAE，∠2=180°﹣∠ABC，∠3=180°﹣∠BCD，∠4=180°﹣∠CDE，∠5=180°﹣∠DEA，然后根据三角形的内角和定理，求出五边形ABCDE的内角和是多少，再用180°×5减去五边形ABCDE的内角和，求出∠1+∠2+∠3+∠4+∠5等于多少即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD是平行四边形，DE平分∠ADC交AB于点E，BF平分∠ABC，交CD于点F．

    (1)、求证：DE=BF；(2)、连接EF，写出图中所有的全等三角形．（不要求证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC在直角坐标系中，

    （1）请写出△ABC各点的坐标．

    （2）若把△ABC向上平移2个单位，再向左平移1个单位得到△A′B′C′，写出 A′、B′、C′的坐标，并在图中画出平移后图形．

    （3）求出三角形ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学改革学生的学习模式，变“老师要学生学习”为“学生自主学习”，培养了学生自主学习的能力．小华与小明同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学，根据收集到的数据绘制了以下两个不完整的统计图（如图）．

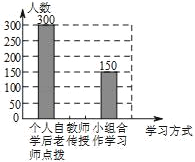
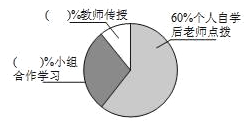
    请根据上面两个不完整的统计图回答以下4个问题：

    （1）这次抽样调查中，共调查了_____名学生．

    （2）补全条形统计图中的缺项．

    （3）在扇形统计图中，选择教师传授的占_____%，选择小组合作学习的占_____%．

    （4）根据调查结果，估算该校1800名学生中大约有_____人选择小组合作学习模式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC和△DCE均是等腰三角形，CA＝CB,CD＝CE,∠BCA＝∠DCE.

    （1）求证：BD＝AE；

    （2）若∠BAC＝70°，求∠BPE的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（2011贵州安顺，10，3分）一只跳蚤在第一象限及x轴、y轴上跳动，在第一秒钟，它从原点跳动到(0，1)，然后接着按图中箭头所示方向跳动[即(0，0)→(0，1) →(1，1) →（1，0）→…]，且每秒跳动一个单位，那么第35秒时跳蚤所在位置的坐标是（ ）

    A. (4，O) B. (5，0) C. (0，5) D. (5，5)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC=11，∠BAC=120°，AD是△ABC的中线，AE是∠BAD的角平分线，DF∥AB交AE的延长线于点F，则DF的长为 ．

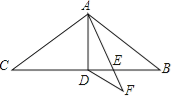
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx过A（4，0），B（1，3）两点，点C、B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H．

    （1）求抛物线的表达式；
    （2）直接写出点C的坐标，并求出△ABC的面积；
    （3）点P是抛物线上一动点，且位于第四象限，当△ABP的面积为6时，求出点P的坐标；
    （4）若点M在直线BH上运动，点N在x轴上运动，当以点C、M、N为顶点的三角形为等腰直角三角形时，请直接写出此时△CMN的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

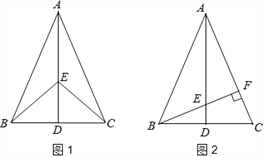
    【题目】如图1，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．

    （1）求证：BE=CE；

    （2）如图2，若BE的延长线交AC于点F，且BF⊥AC，垂足为F，∠BAC=45°，原题设其它条件不变．求证：△AEF≌△BCF．

    查看答案和解析>>

    同步练习册答案