
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C,且B(1,0),C(0,3),将△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.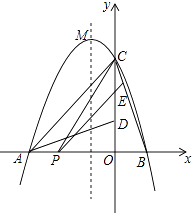
(1)求该二次函数的解析式;
(2)若点P为线段AB上的任一动点,过点P作PE∥AC,交BC于点E,连结CP,求△PCE面积S的最大值;
(3)设抛物线的顶点为M,Q为它的图象上的任一动点,若△OMQ为以OM为底的等腰三角形,求Q点的坐标.
【答案】
(1)
解:∵B(1,0),C(0,3),
∴OB=1,OC=3.
∵△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.
∴OA=OC=3,
∴A(﹣3,0),
∵点A,B,C在抛物线上,
∴ 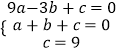 ,
,
∴ 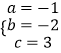 ,
,
∴二次函数的解析式为y=﹣x2﹣2x+3
(2)
解:设点P(x,0),则PB=1﹣x,
∵A(﹣3,0),B(1,0),
∴AB=4,
∵C(0,3),
∴OC=3,
∴S△ABC= ![]() AB×OC=6,
AB×OC=6,
∵PE∥AC,
∴△BPE∽△BAC,
∴ ![]() ,
,
∴S△PBE= ![]() (1﹣x)2,
(1﹣x)2,
∴S△PCE=S△PBC﹣S△PBE= ![]() PB×OC﹣
PB×OC﹣ ![]() (1﹣x)2=
(1﹣x)2= ![]() (1﹣x)×3﹣
(1﹣x)×3﹣ ![]() (1﹣x)2=﹣
(1﹣x)2=﹣ ![]() (x+1)2+
(x+1)2+ ![]() ,
,
当x=﹣1时,S△PCE的最大值为 ![]()
(3)
解:∵二次函数的解析式为y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点坐标(﹣1,4),
∵△OMQ为等腰三角形,OM为底,
∴MQ=OQ,
∴ ![]() =
= ![]() ,
,
∴8x2+18x=7=0,
∴x= ![]() ,
,
∴y= ![]() 或y=
或y= ![]() ,
,
∴Q( ![]() ,
, ![]() ),或(
),或( ![]() ,
, ![]() )
)
【解析】(1)先求出点A坐标,再用待定系数法求出抛物线解析式;(2)先求出S△PCE=S△PBC﹣S△PBE=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,即可求出最大面积;(3)先求出抛物线顶点坐标,由等腰三角形的两腰相等建立方程求出点Q坐标.
,即可求出最大面积;(3)先求出抛物线顶点坐标,由等腰三角形的两腰相等建立方程求出点Q坐标.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】2013年是一个让人记忆犹新的年份,雾霾天气持续笼罩我国大部分地区,口罩市场出现热销,某旗舰网店用8000元购进甲、乙两种型号的口罩,销售完后共获利2800元,进价和售价如下表:
品名 价格 | 甲型口罩 | 乙型口罩 |
进价(元/袋) | 20 | 25 |
售价(元/袋) | 26 | 35 |
(1)求该网店购进甲、乙两种型号口罩各多少袋?
(2)该网店第二次以原价购进甲、乙两种型号口罩,购进乙种型号口罩袋数不变,而购进甲种型号口罩袋数是第一次的2倍.甲种口罩按原售价出售,而乙种口罩让利销售.若两种型号的口罩都售完,要使第二次销售活动获利不少于3680元,乙种型号的口罩最低售价为每袋多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如表:
选手 | 选拔成绩/环 | 中位数 | 平均数 | |||||
甲 | 10 | 9 | 8 | 8 | 10 | 9 | ||
乙 | 10 | 10 | 8 | 10 | 7 | 9 | ||
(1)把表中所空各项数据填写完整;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1),(2)计算的结果,你认为推荐谁参加省比赛更合适?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如图2所示.

图1 图2
(1)你认为这个零件符合要求吗?为什么?
(2)求这个零件的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下两个不完整的统计图(如图).
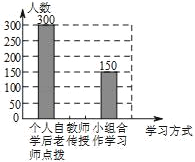
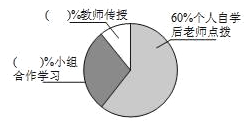
请根据上面两个不完整的统计图回答以下4个问题:
(1)这次抽样调查中,共调查了_____名学生.
(2)补全条形统计图中的缺项.
(3)在扇形统计图中,选择教师传授的占_____%,选择小组合作学习的占_____%.
(4)根据调查结果,估算该校1800名学生中大约有_____人选择小组合作学习模式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DCE均是等腰三角形,CA=CB,CD=CE,∠BCA=∠DCE.

(1)求证:BD=AE;
(2)若∠BAC=70°,求∠BPE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为 .
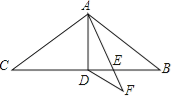
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图. 最喜爱的传统文化项目类型频数分布表
项目类型 | 频数 | 频率 |
书法类 | 18 | a |
围棋类 | 14 | 0.28 |
喜剧类 | 8 | 0.16 |
国画类 | b | 0.20 |
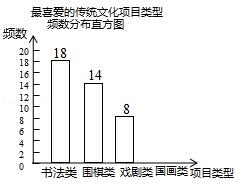
根据以上信息完成下列问题:
(1)频数分布表中a= , b=;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com