
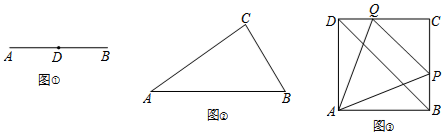
分析 (1)如图1中,作射线DN,在射线DN上截取DC=AB,连接AC、BC,则△ABC即为所求.
(2)如图2中,取AC的中点D,连接BD.由∠ACB=90°,tanA=$\frac{{\sqrt{3}}}{2}$=$\frac{BC}{AC}$,所以可以假设BC=$\sqrt{3}$k,AC=2k,则CD=AD=k,在Rt△BDC中,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{(\sqrt{3}k)^{2}+{k}^{2}}$=2k,即可证明BD=AC.
(3)如图3中,连接AC,交PQ于M.设DQ=x.首先证明CQ=CP,DQ=PB,根据AM=PQ列出方程即可解决问题.
解答 解:(1)如图1中,作射线DN,在射线DN上截取DC=AB,连接AC、BC,则△ABC即为所求.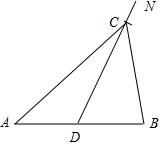
(2)如图2中,取AC的中点D,连接BD.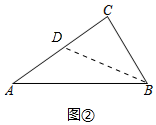
∵∠ACB=90°,tanA=$\frac{{\sqrt{3}}}{2}$,
∴可以假设BC=$\sqrt{3}$k,AC=2k,
∴CD=AD=k,
在Rt△BDC中,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{(\sqrt{3}k)^{2}+{k}^{2}}$=2k,
∴BD=AC,
∴△ABC是“等中三角形”;
(3)如图3中,连接AC,交PQ于M.设DQ=x.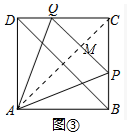
∵四边形ABCD是正方形,
∴∠CDB=∠CB=45°,CD=BC=AB=6,
∵PQ∥BD,
∴∠CQP=∠CPQ=45°,
∴CQ=CP,DQ=PB=x,
∴CQ=CP=6-x,PQ=$\sqrt{2}$(6-x),CM=$\frac{\sqrt{2}}{2}$(6-x),
由题意AM=PQ,
∴6$\sqrt{2}$-$\frac{\sqrt{2}}{2}$(6-x)=$\sqrt{2}$(6-x),
∴x=2,
∴DQ=2.
点评 本题考查四边形综合题、三角形的中线的定义、正方形的性质、等腰直角三角形的判定和性质、锐角三角函数、勾股定理等知识,解题的关键是理解题意,学会用方程的思想思考问题,属于中考创新题目.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 绝对值等于其本身的有理数只有0,1 | |
| B. | 相反数等于其本身的有理数只有零 | |
| C. | 倒数等于其本身的有理数只有1 | |
| D. | 最小的数是零 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
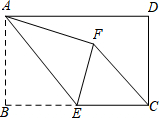 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为$\frac{18}{5}$.
如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为$\frac{18}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com