
 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
| 第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
| 路程(km) | -8 | -11 | -14 | 0 | -16 | +41 | +8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
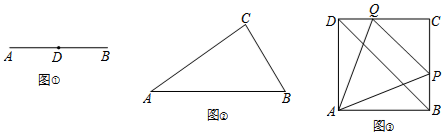
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
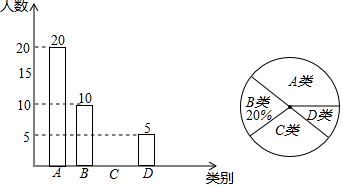
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有一抛物线型的立交桥桥拱,这个桥拱的最大高度为16米,跨度为40米,若要在跨度中心点M的左,右5米处各垂直竖立一根铁柱支撑拱顶,则铁柱应取多长?
如图,有一抛物线型的立交桥桥拱,这个桥拱的最大高度为16米,跨度为40米,若要在跨度中心点M的左,右5米处各垂直竖立一根铁柱支撑拱顶,则铁柱应取多长?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com