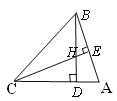
【题目】如图，在△ABC中，∠A︰∠B︰∠C=5︰4︰3，BD、CE分别是边AC、AB上的高，BD、CE相交于点H，求∠BHC的度数.
【答案】105°
【解析】试题分析：本题先根据三角形内角和定理，求出△ABC三个内角的度数；然后利用垂直定义及四边形AEHD的内角和等于360°，求出∠EHD的度数，即∠BHC的度数．
试题解析：解：在△ABC中，∵∠A=5x°，∠ABC=4x°，∠ACB=3x°．
又∵∠A+∠ABC+∠ACB=180°，∴5x°+4x°+3x°=180°，解得x=15，∠A=5x°=75°，∵BD，CE分别是边AC，AB上的高，∴∠ADB=90°，∠BEC=90°，∵在四边形AEHD中，∠DHE=360°﹣∠ADB﹣∠AEC﹣∠A=360°﹣90°﹣90°﹣75°=105°，∴∠BHC=∠DHE =105°．
科目：初中数学 来源： 题型：
【题目】2020年3月9日，中国第54颗北斗导航卫星成功发射，其轨道高度约为36000000m．数36000000用科学记数法表示为（ ）
A.0.36×108B.36×107C.3.6×108D.3.6×107
查看答案和解析>>
科目：初中数学 来源： 题型：
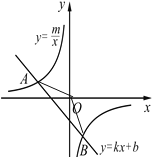
【题目】如图，已知A(-4，2)、B(n，-4)是一次函数
的图象与反比例函数
的图象的两个交点.
（1）求此反比例函数和一次函数的解析式；
（2）求△AOB的面积；
（3）根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，在△ABC中，∠BAC=90°，∠ABC=45°，点D为直线BC上一动点（点D不与点B、C重合）．以AD为边做正方形ADEF，连接CF．
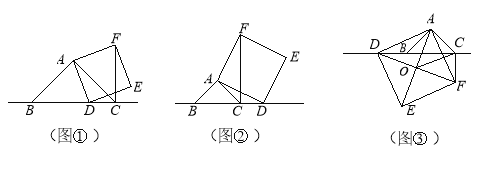
（1）如图①，当点D在线段BC上时，求证：CF+CD=BC；
（2）如图②，当点D在线段BC的延长线上时，其他条件不变，请直接写出CF、BC、CD三条线段之间的关系；
（3）如图③，当点D在线段BC的反向延长线上时，且点A、F分别在直线BC的两侧，其他条件不变；
①请直接写出CF、BC、CD三条线段之间的关系；
②若正方形ADEF的边长为
，对角线AE、DF相交于点O，连接OC．求OC的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，已知A
，B
，C
三点，其中a、b、c满足关系式
， 
.
(1) a= ；b= ；c= .
(2) 如果在第二象限内有一点P
，请用含
的式子表示四边形ABOP的面积；
(3) 在(2)的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为迎接“义务教育均衡发展”检查，我市抽查了某校七年级8个班的班额人数，抽查数据统计如下：52，49，56，54，52，51，55，54，这四组数据的众数是（ ）
A.52和54
B.52
C.53
D.54
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com