
����Ŀ����֪������ABC�У���BAC=90������ABC=45������DΪֱ��BC��һ���㣨��D�����B��C�غϣ�����ADΪ����������ADEF������CF��
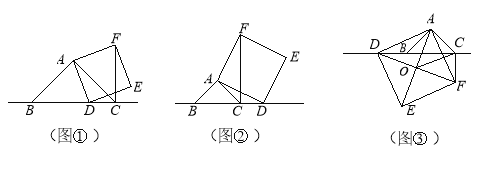
��1����ͼ��������D���߶�BC��ʱ����֤��CF+CD=BC��
��2����ͼ��������D���߶�BC���ӳ�����ʱ�������������䣬��ֱ��д��CF��BC��CD�����߶�֮��Ĺ�ϵ��
��3����ͼ��������D���߶�BC�ķ����ӳ�����ʱ���ҵ�A��F�ֱ���ֱ��BC�����࣬�����������䣻
����ֱ��д��CF��BC��CD�����߶�֮��Ĺ�ϵ��
����������ADEF�ı߳�Ϊ![]() ���Խ���AE��DF�ཻ�ڵ�O������OC����OC�ij�����
���Խ���AE��DF�ཻ�ڵ�O������OC����OC�ij�����
���𰸡�(1)��֤�����̼�������(2)��CF��CD=BC��(3)��CD��CF=BC��2.
��������
���������(1)�����������ε������ж�����BAD����CAFȫ�ȣ��Ӷ��ó�BD=CF������BD+CD=BC�ó��𰸣�(2)������ͼ�εó��߶�֮��Ĺ�ϵ��(3)�����ȸ��������ε�����֤����BAD����CAFȫ�ȣ�Ȼ��ó���ACF=��ABD=135�����Ӷ�˵����FCDΪֱ�������Σ����������εĶԽ��ߵó�DF�ij��ȣ�Ȼ�����ֱ��������б���ϵ����ߵ����ʵó�OC�ij���.
���������(1)���ߡ�BAC=90������ABC=45�������ACB=��ABC=45������AB=AC��
���ı���ADEF�������Σ���AD=AF����DAF=90����
�ߡ�BAD=90��-��DAC����CAF=90��-��DAC�����BAD=��CAF��
������BAD����CAF��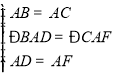 ���BAD �� ��CAF��SAS������BD=CF��
���BAD �� ��CAF��SAS������BD=CF��
��BD+CD=BC����CF+CD=BC��
(2)��CF��CD=BC
(3)����CD��CF =BC��
�ڡߡ�BAC=90������ABC=45�������ACB=��ABC=45������AB=AC�� ���ı���ADEF�������Σ�
��AD=AF����DAF=90���� �ߡ�BAD=90��-��BAF����CAF=90��-��BAF�����BAD=��CAF��
������BAD����CAF��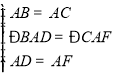 ���BAD �� ��CAF��SAS����
���BAD �� ��CAF��SAS����
���ABD=��ACF���ߡ�ABC=45������ABD=135���� ���ACF=��ABD=135����
���FCD=90�������FCD��ֱ�������Σ� ��������ADEF�ı߳�Ϊ![]() �ҶԽ���AE��DF�ཻ�ڵ�O��
�ҶԽ���AE��DF�ཻ�ڵ�O��
��DF=![]() AD=4��OΪDF�е㣮 ��OC=
AD=4��OΪDF�е㣮 ��OC=![]() DF=2��
DF=2��


 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ع�α���������ѧϰ��һ��������ʵ������ֱ�߱�һ��ƽ�������أ����õĶ�Ӧ�߶γɱ�����
���������顿
��1����ͼ1������ABC�У���D��F��AB�ϣ�E��G��AC�ϣ�DE��FC��BC����AD=2��AE=1��DF=6����EG= �� ![]() = ��
= ��
��2����ͼ2������ABC �У���D��F��AB�ϣ�E��G��AC�ϣ���DE��BC��FG����AD��DF��FBΪ�߹�����ADM����AM=BF��MD=DF������AE��EG��GCΪ�߹�����AEN����AN=GC��NE=EG����
��֤����M=��N��
������̽����
����������ʵ�������ǿ����á�ƽ���߷��߶γɱ���������������⣺
��3����ͼ3����֪��ABC���߶�a������ֱ����Բ������A��B��C�䣮
���㣺����A��B��C���ס�ABC������A��B��C����ܳ������߶�a�ij��ȣ���������ͼ�ۼ�����д����ͼ���裩

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
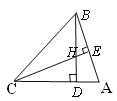
����Ŀ����ͼ������ABC�У���A�U��B�U��C=5�U4�U3��BD��CE�ֱ��DZ�AC��AB�ϵĸߣ�BD��CE�ཻ�ڵ�H������BHC�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪AB��һ��ֻ��3�׳���խ��·������һ��С������һ������AB�����������뵹�����ܼ���ͨ�������С������AB��������ʻ��10���ӣ�����AB��������ʻ��20���ӣ�С������AB�ε������ٶ�����������ʻ�ٶȵ� ![]() ������AB�ε������ٶ�����������ʻ��
������AB�ε������ٶ�����������ʻ�� ![]() ��С�����赹����·���Ǵ���4������������ͨ��AB�����խ·������ʱ�������ӣ�
��С�����赹����·���Ǵ���4������������ͨ��AB�����խ·������ʱ�������ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С�����˳���á������Ű����и�������������_____��
1.6����1.6��0��3����3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߶�AB=30cm��
��1����ͼ1����P���߶�AB�Ե�A���B��2cm/s���ٶ��˶���ͬʱ��Q���߶�BA�Ե�B���A��3cm/s���ٶ��˶��������Ӻ�P��Q����������
��2�������P��Q�������10cm��
��3����ͼ2��AO=PO=4cm����POB=60�㣬�ֵ�P���ŵ�O��30��/����ٶ���ʱ����תһ��ֹͣ��ͬʱ��Q��ֱ��B��B����A���˶���������P��Q���������������Q���˶��ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������⡰��ֱ��ͬһֱ�ߵ�����ֱ����ƽ�С���д�ɡ����������ô��������ʽΪ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com