
【题目】已知线段AB=30cm.
(1)如图1,点P沿线段AB自点A向点B以2cm/s的速度运动,同时点Q沿线段BA自点B向点A以3cm/s的速度运动,几秒钟后,P,Q两点相遇?
(2)几秒后,点P、Q两点相距10cm?
(3)如图2,AO=PO=4cm,∠POB=60°,现点P绕着点O以30°/秒的速度逆时针旋转一周停止,同时点Q沿直线B自B点向A点运动,假若点P,Q两点能相遇,求点Q的运动速度.
【答案】
(1)
解:设经过ts后,点P、Q相遇.
依题意,有2t+3t=30,
解得:t=6.
答:经过6秒钟后,点P、Q相遇
(2)
解:设经过xs,P、Q两点相距10cm,由题意得
2x+3x+10=30或2x+3x﹣10=30,
解得:x=4或x=8.
答:经过4秒钟或8秒钟后,P、Q两点相距10cm
(3)
解:点P,Q只能在直线AB上相遇,
则点P旋转到直线AB上的时间为![]() =4(s)或
=4(s)或![]() =10(s)
=10(s)
设点Q的速度为y cm/s,则有4y=30,解得 y=![]() ;
;
或10y=30﹣8,解得y=![]()
答:点Q的速度为![]() cm/s或
cm/s或![]() cm/s.
cm/s.
【解析】(1)根据相遇时,点P和点Q的运动的路程和等于AB的长列方程即可求解;(2)设经过xs,P、Q两点相距10cm,分相遇前和相遇后两种情况建立方程求出其解即可;(3)由于点P,Q只能在直线AB上相遇,而点P旋转到直线AB上的时间分2种情况,所以根据题意列出方程分别求解.


科目:初中数学 来源: 题型:
【题目】2020年3月9日,中国第54颗北斗导航卫星成功发射,其轨道高度约为36000000m.数36000000用科学记数法表示为( )
A.0.36×108B.36×107C.3.6×108D.3.6×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B、C重合).以AD为边做正方形ADEF,连接CF.
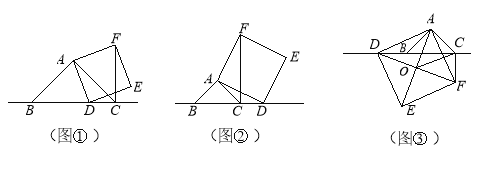
(1)如图①,当点D在线段BC上时,求证:CF+CD=BC;
(2)如图②,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF、BC、CD三条线段之间的关系;
(3)如图③,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其他条件不变;
①请直接写出CF、BC、CD三条线段之间的关系;
②若正方形ADEF的边长为![]() ,对角线AE、DF相交于点O,连接OC.求OC的长度.
,对角线AE、DF相交于点O,连接OC.求OC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A![]() ,B
,B![]() ,C
,C![]() 三点,其中a、b、c满足关系式
三点,其中a、b、c满足关系式![]() ,
, ![]() .
.
(1) a= ;b= ;c= .
(2) 如果在第二象限内有一点P![]() ,请用含
,请用含![]() 的式子表示四边形ABOP的面积;
的式子表示四边形ABOP的面积;
(3) 在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
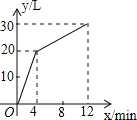
【题目】一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,求:
(1) 出水管每分钟的出水量是多少(L);
(2) 第8分钟时,容器内的水量是多少(L).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学测验中,某小组五位同学的成绩分别是:110,105,90,95,90,则这五个数据的中位数是( )
A.90
B.95
C.100
D.105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
(1)现随机转动转盘一次,停止后,指针指向1的概率为 ;
(2)小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“义务教育均衡发展”检查,我市抽查了某校七年级8个班的班额人数,抽查数据统计如下:52,49,56,54,52,51,55,54,这四组数据的众数是( )
A.52和54
B.52
C.53
D.54
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com