
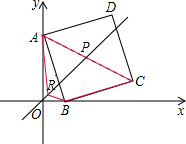
 如图,点A在y轴上,点B在x轴上,以AB为边作正方形ABCD,P为正方形ABCD的对称中心,正方形ABCD的边长为
如图,点A在y轴上,点B在x轴上,以AB为边作正方形ABCD,P为正方形ABCD的对称中心,正方形ABCD的边长为| 10 |
| 2 |
| OA |
| OB |
| 10 |
| 13 |
| 5 |
| ||
| 5 |
| ||
| 5 |
| OA |
| OB |
| 10 |
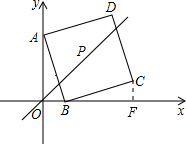 ∴在△AOB中,OA2+OB2=AB2,即9x2+x2=(
∴在△AOB中,OA2+OB2=AB2,即9x2+x2=(| 10 |
|
|
|
| 5 |
| 6 |
| 23 |
| 6 |
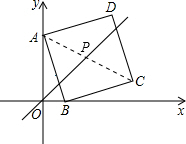 (2)连接AC.
(2)连接AC.| 0+4 |
| 2 |
| 3+1 |
| 2 |
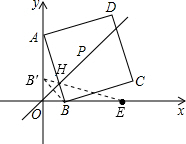 (3)在直线OP上存在一点H,能够使△BHE的周长最小.
(3)在直线OP上存在一点H,能够使△BHE的周长最小.| 5 |
| 6 |
| 23 |
| 6 |
| 5 |
| 6 |
| 23 |
| 6 |
| 18 |
| 5 |
| 18 |
| 5 |
| 18 |
| 5 |
| 13 |
| 5 |
| OB′2+OE2 |
12+(
|
| ||
| 5 |
| ||
| 5 |
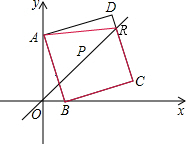 (4)以A、B、C、R为顶点的梯形,有三种可能:
(4)以A、B、C、R为顶点的梯形,有三种可能:| 13 |
| 4 |
| 13 |
| 4 |
| 13 |
| 4 |
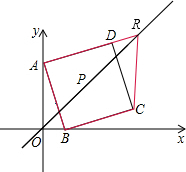 ②如果AR∥BC,那么R是直线OP与AD延长线的交点.
②如果AR∥BC,那么R是直线OP与AD延长线的交点.| 1 |
| 3 |
| 1 |
| 3 |
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
 ∴可求得直线AC的解析式为:y=-
∴可求得直线AC的解析式为:y=-| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 13 |
| 4 |
| 9 |
| 2 |
| 1 |
| 3 |


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
| 5 |
| 6 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 在直角坐标系中,有两个点A(-6,3),B(-2,5).在y轴上找一个点C,在x轴上找一点D,画出四边形ABCD,使其周长最短(保留作图痕迹,不要求证明)
在直角坐标系中,有两个点A(-6,3),B(-2,5).在y轴上找一个点C,在x轴上找一点D,画出四边形ABCD,使其周长最短(保留作图痕迹,不要求证明)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com