
【题目】在如图所示的网格中有四条线段AB、CD、EF、GH(线段端点在格点上),
⑴选取其中三条线段,使得这三条线段能围成一个直角三角形.
答:选取的三条线段为 .
⑵只变动其中两条线段的位置,在原图中画出一个满足上题的直角三角形(顶点仍在格点,并标上必要的字母).
答:画出的直角三角形为△ .
⑶所画直角三角形的面积为 .

科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BCAD= ![]() AE2;④S△ABC=4S△ADF . 其中正确的有( )
AE2;④S△ABC=4S△ADF . 其中正确的有( ) 
A.1个
B.2 个
C.3 个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
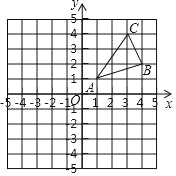
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)若△A1B1C1与△ABC关于y轴成轴对称,则△A1B1C1三个顶点坐标分别为A1_____,B1_____,C1_____
(2)在y轴上是否存在点Q.使得S△ACQ=![]() S△ABC,如果存在,求出点Q的坐标,如果不存在,说明理由;
S△ABC,如果存在,求出点Q的坐标,如果不存在,说明理由;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点. 
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠ACB=90°,AC=BC,AE 是 BC 边的中线,过点C 作 CF⊥AE,垂足为点 F,过点 B 作 BD⊥BC 交 CF 的延长线于点 D.
(1)试证明:AE=CD;
(2)若 AC=12cm,求线段 BD 的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系xoy中,直线l:y=kx+b交x轴,y轴于点E,F,点B的坐标是(2,2),过点B分别作x轴、y轴的垂线,垂足为A、C,点D是线段CO上的动点,以BD为对称轴,作与△BCD或轴对称的△BC′D.
(1)当∠CBD=15°时,求点C′的坐标.
(2)当图1中的直线l经过点A,且k=﹣ ![]() 时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
(3)当图1中的直线l经过点D,C′时(如图3),以DE为对称轴,作于△DOE或轴对称的△DO′E,连结O′C,O′O,问是否存在点D,使得△DO′E与△CO′O相似?若存在,求出k、b的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个长为8分米,宽为5分米,高为7分米的长方体上,截去一个长为6分米,宽为5分米,深为2分米的长方体后,得到一个如图所示的几何体.一只蚂蚁要从该几何体的顶点A处,沿着几何体的表面到几何体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是 分米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com