
【题目】如图,已知抛物线y= ![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点. 
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
【答案】
(1)
解:∵点A(0,1).B(﹣9,10)在抛物线上,
∴ 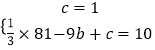 ,
,
∴ ![]() ,
,
∴抛物线的解析式为y= ![]() x2+2x+1
x2+2x+1
(2)
解:∵AC∥x轴,A(0,1)
∴ ![]() x2+2x+1=1,
x2+2x+1=1,
∴x1=6,x2=0,
∴点C的坐标(﹣6,1),
∵点A(0,1).B(﹣9,10),
∴直线AB的解析式为y=﹣x+1,
设点P(m, ![]() m2+2m+1)
m2+2m+1)
∴E(m,﹣m+1)
∴PE=﹣m+1﹣( ![]() m2+2m+1)=﹣
m2+2m+1)=﹣ ![]() m2﹣3m,
m2﹣3m,
∵AC⊥EP,AC=6,
∴S四边形AECP
=S△AEC+S△APC
= ![]() AC×EF+
AC×EF+ ![]() AC×PF
AC×PF
= ![]() AC×(EF+PF)
AC×(EF+PF)
= ![]() AC×PE
AC×PE
= ![]() ×6×(﹣
×6×(﹣ ![]() m2﹣3m)
m2﹣3m)
=﹣m2﹣9m
=﹣(m+ ![]() )2+
)2+ ![]() ,
,
∵﹣6<m<0
∴当m=﹣ ![]() 时,四边形AECP的面积的最大值是
时,四边形AECP的面积的最大值是 ![]() ,
,
此时点P(﹣ ![]() ,﹣
,﹣ ![]() ).
).
(3)
解:∵y= ![]() x2+2x+1=
x2+2x+1= ![]() (x+3)2﹣2,
(x+3)2﹣2,
∴P(﹣3,﹣2),
∴PF=yF﹣yP=3,CF=xF﹣xC=3,
∴PF=CF,
∴∠PCF=45°
同理可得:∠EAF=45°,
∴∠PCF=∠EAF,
∴在直线AC上存在满足条件的Q,
设Q(t,1)且AB=9 ![]() ,AC=6,CP=3
,AC=6,CP=3 ![]()
∵以C、P、Q为顶点的三角形与△ABC相似,
①当△CPQ∽△ABC时,
∴ ![]() ,
,
∴ ![]() ,
,
∴t=﹣4,
∴Q(﹣4,1)
②当△CQP∽△ABC时,
∴ ![]() ,
,
∴ ![]() ,
,
∴t=3,
∴Q(3,1).
【解析】(1)用待定系数法求出抛物线解析式即可;
(2)设点P(m, ![]() m2+2m+1),表示出PE=﹣
m2+2m+1),表示出PE=﹣ ![]() m2﹣3m,再用S四边形AECP=S△AEC+S△APC=
m2﹣3m,再用S四边形AECP=S△AEC+S△APC= ![]() AC×PE,建立函数关系式,求出极值即可;
AC×PE,建立函数关系式,求出极值即可;
(3)先判断出PF=CF,再得到∠PCF=∠EAF,以C、P、Q为顶点的三角形与△ABC相似,分两种情况计算即可.此题是二次函数综合题,主要考查了待定系数法,相似三角形的性质,几何图形面积的求法(用割补法),解本题的关键是求函数解析式.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】某学校举行“社会主义核心价值观”知识比赛活动,全体学生都参加比赛,学校对参赛学生均给与表彰,并设置一、二、三等奖和纪念奖共四个奖项,赛后将获奖情况绘制成如下所示的两幅不完整的统计图,请根据图中所给的信息,解答下列问题: 
(1)该校共有名学生;
(2)在图①中,“三等奖”所对应扇形的圆心角度数是;
(3)将图②补充完整;
(4)从该校参加本次比赛活动的学生中随机抽查一名.求抽到获得一等奖的学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=x2﹣3x+m,直线l:y=kx(k>0),当k=1时,抛物线C与直线l只有一个公共点.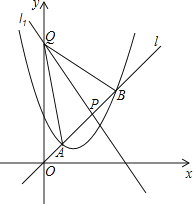
(1)求m的值;
(2)若直线l与抛物线C交于不同的两点A,B,直线l与直线l1:y=﹣3x+b交于点P,且 ![]() +
+ ![]() =
= ![]() ,求b的值;
,求b的值;
(3)在(2)的条件下,设直线l1与y轴交于点Q,问:是否在实数k使S△APQ=S△BPQ?若存在,求k的值,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.
(1)求抛物线的解析式及点C的坐标;
(2)求证:△ABC是直角三角形;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中
中![]() ,
, ![]() 于点
于点![]() ,
, ![]() 于点
于点![]() ,
, ![]() 为
为![]() 边的中点,连接
边的中点,连接![]() 、
、![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() 为等边三角形.下面判断正确是( )
为等边三角形.下面判断正确是( )

A. ①正确 B. ②正确
C. ①②都正确 D. ①②都不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的网格中有四条线段AB、CD、EF、GH(线段端点在格点上),
⑴选取其中三条线段,使得这三条线段能围成一个直角三角形.
答:选取的三条线段为 .
⑵只变动其中两条线段的位置,在原图中画出一个满足上题的直角三角形(顶点仍在格点,并标上必要的字母).
答:画出的直角三角形为△ .
⑶所画直角三角形的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全球最大的关公塑像矗立在荆州古城东门外.如图,张三同学在东门城墙上C处测得塑像底部B处的俯角为18°48′,测得塑像顶部A处的仰角为45°,点D在观测点C正下方城墙底的地面上,若CD=10米,则此塑像的高AB约为米(参考数据:tan78°12′≈4.8).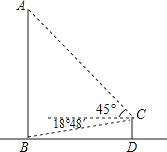
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,已知:点A(﹣2,﹣1)在双曲线C:y= ![]() 上,直线l1:y=﹣x+2,直线l2与l1关于原点成中心对称,F1(2,2),F2(﹣2,﹣2)两点间的连线与曲线C在第一象限内的交点为B,P是曲线C上第一象限内异于B的一动点,过P作x轴平行线分别交l1 , l2于M,N两点.
上,直线l1:y=﹣x+2,直线l2与l1关于原点成中心对称,F1(2,2),F2(﹣2,﹣2)两点间的连线与曲线C在第一象限内的交点为B,P是曲线C上第一象限内异于B的一动点,过P作x轴平行线分别交l1 , l2于M,N两点.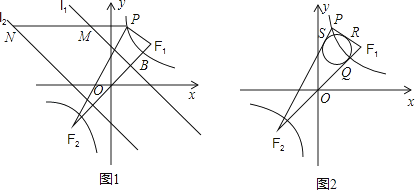
(1)求双曲线C及直线l2的解析式;
(2)求证:PF2﹣PF1=MN=4;
(3)如图2所示,△PF1F2的内切圆与F1F2 , PF1 , PF2三边分别相切于点Q,R,S,求证:点Q与点B重合.(参考公式:在平面坐标系中,若有点A(x1 , y1),B(x2 , y2),则A、B两点间的距离公式为AB= ![]() .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com